Gene co-expression network

A gene co-expression network (GCN) is an undirected graph, where each node corresponds to a gene, and a pair of nodes is connected with an edge if there is a significant co-expression relationship between them.[1] Having gene expression profiles of a number of genes for several samples or experimental conditions, a gene co-expression network can be constructed by looking for pairs of genes which show a similar expression pattern across samples, since the transcript levels of two co-expressed genes rise and fall together across samples. Gene co-expression networks are of biological interest since co-expressed genes are controlled by the same transcriptional regulatory program, functionally related, or members of the same pathway or protein complex.[2]

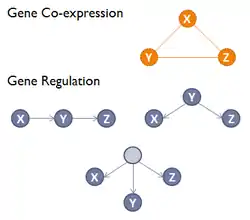
A gene co-expression network constructed from a microarray dataset containing gene expression profiles of 7221 genes for 18 gastric cancer patients

The direction and type of co-expression relationships are not determined in gene co-expression networks; whereas in a gene regulatory network (GRN) a directed edge connects two genes, representing a biochemical process such as a reaction, transformation, interaction, activation or inhibition.[3] Compared to a GRN, a GCN does not attempt to infer the causality relationships between genes and in a GCN the edges represent only a correlation or dependency relationship among genes.[4] Modules or the highly connected subgraphs in gene co-expression networks correspond to clusters of genes that have a similar function or involve in a common biological process which causes many interactions among themselves.[3]

The direction of edges is overlooked in gene co-expression networks. While three genes X, Y and Z are found to be co-expressed, it is not determined whether X activates Y and Y activates Z, or Y activates X and Z, or another gene activates three of them.

Gene co-expression networks are usually constructed using datasets generated by high-throughput gene expression profiling technologies such as Microarray or RNA-Seq. Recently, co-expression networks are used to analyze single cell RNA-Seq data, in order to better characterize the gene to gene relations in a cohort of cells from a specific cell type.

History

The concept of gene co-expression networks was first introduced by Butte and Kohane in 1999 as relevance networks.[5] They gathered the measurement data of medical laboratory tests (e.g. hemoglobin level ) for a number of patients and they calculated the Pearson correlation between the results for each pair of tests and the pairs of tests which showed a correlation higher than a certain level were connected in the network (e.g. insulin level with blood sugar). Butte and Kohane used this approach later with mutual information as the co-expression measure and using gene expression data for constructing the first gene co-expression network.[6]

Constructing gene co-expression networks

A good number of methods have been developed for constructing gene co-expression networks. In principle, they all follow a two step approach: calculating co-expression measure, and selecting significance threshold. In the first step, a co-expression measure is selected and a similarity score is calculated for each pair of genes using this measure. Then, a threshold is determined and gene pairs which have a similarity score higher than the selected threshold are considered to have a significant co-expression relationship and are connected by an edge in the network.

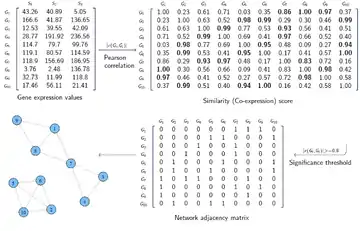
The two general steps for constructing a gene co-expression network: calculating co-expression score (e.g. the absolute value of Pearson correlation coefficient) for each pair of genes, and selecting a significance threshold (e.g. correlation > 0.8).

The input data for constructing a gene co-expression network is often represented as a matrix. If we have the gene expression values of m genes for n samples (conditions), the input data would be an m×n matrix, called expression matrix. For instance, in a microarray experiment the expression values of thousands of genes are measured for several samples. In first step, a similarity score (co-expression measure) is calculated between each pair of rows in expression matrix. The resulting matrix is an m×m matrix called the similarity matrix. Each element in this matrix shows how similarly the expression levels of two genes change together. In the second step, the elements in the similarity matrix which are above a certain threshold (i.e. indicate significant co-expression) are replaced by 1 and the remaining elements are replaced by 0. The resulting matrix, called the adjacency matrix, represents the graph of the constructed gene co-expression network. In this matrix, each element shows whether two genes are connected in the network (the 1 elements) or not (the 0 elements).

Co-expression measure

The expression values of a gene for different samples can be represented as a vector, thus calculating the co-expression measure between a pair of genes is the same as calculating the selected measure for two vectors of numbers.

Pearson's correlation coefficient, Mutual Information, Spearman's rank correlation coefficient and Euclidean distance are the four mostly used co-expression measures for constructing gene co-expression networks. Euclidean distance measures the geometric distance between two vectors, and so considers both the direction and the magnitude of the vectors of gene expression values. Mutual information measures how much knowing the expression levels of one gene reduces the uncertainty about the expression levels of another. Pearson’s correlation coefficient measures the tendency of two vectors to increase or decrease together, giving a measure of their overall correspondence. Spearman's rank correlation is the Pearson’s correlation calculated for the ranks of gene expression values in a gene expression vector.[2] Several other measures such as partial correlation,[7] regression,[8] and combination of partial correlation and mutual information[9] have also been used.

Each of these measures have their own advantages and disadvantages. The Euclidean distance is not appropriate when the absolute levels of functionally related genes are highly different. Furthermore, if two genes have consistently low expression levels but are otherwise randomly correlated, they might still appear close in Euclidean space.[2] One advantage to mutual information is that it can detect non-linear relationships; however this can turn into a disadvantage because of detecting sophisticated non-linear relationships which does not look biologically meaningful. In addition, for calculating mutual information one should estimate the distribution of the data which needs a large number of samples for a good estimate. Spearman’s rank correlation coefficient is more robust to outliers, but on the other hand it is less sensitive to expression values and in datasets with small number of samples may detect many false positives.

Pearson’s correlation coefficient is the most popular co-expression measure used in constructing gene co-expression networks. The Pearson's correlation coefficient takes a value between -1 and 1 where absolute values close to 1 show strong correlation. The positive values correspond to an activation mechanism where the expression of one gene increases with the increase in the expression of its co-expressed gene and vice versa. When the expression value of one gene decreases with the increase in the expression of its co-expressed gene, it corresponds to an underlying suppression mechanism and would have a negative correlation.

There are two disadvantages for Pearson correlation measure: it can only detect linear relationships and it is sensitive to outliers. Moreover, Pearson correlation assumes that the gene expression data follow a normal distribution. Song et al.[10] have suggested biweight midcorrelation (bicor) as a good alternative for Pearson’s correlation. "Bicor is a median based correlation measure, and is more robust than the Pearson correlation but often more powerful than the Spearman's correlation". Furthermore, it has been shown that "most gene pairs satisfy linear or monotonic relationships" which indicates that "mutual information networks can safely be replaced by correlation networks when it comes to measuring co-expression relationships in stationary data[10]".

Threshold selection

Several methods have been used for selecting a threshold in constructing gene co-expression networks. A simple thresholding method is to choose a co-expression cutoff and select relationships which their co-expression exceeds this cutoff. Another approach is to use Fisher’s Z-transformation which calculates a z-score for each correlation based on the number of samples. This z-score is then converted into a p-value for each correlation and a cutoff is set on the p-value. Some methods permute the data and calculate a z-score using the distribution of correlations found between genes in permuted dataset.[2] Some other approaches have also been used such as threshold selection based on clustering coefficient[11] or random matrix theory.[12]

The problem with p-value based methods is that the final cutoff on the p-value is chosen based on statistical routines(e.g. a p-value of 0.01 or 0.05 is considered significant), not based on a biological insight.

WGCNA is a framework for constructing and analyzing weighted gene co-expression networks.[13] The WGCNA method selects the threshold for constructing the network based on the scale-free topology of gene co-expression networks. This method constructs the network for several thresholds and selects the threshold which leads to a network with scale-free topology. Moreover, the WGCNA method constructs a weighted network which means all possible edges appear in the network, but each edge has a weight which shows how significant is the co-expression relationship corresponding to that edge. Of note, threshold selection is intended to coerce networks into a scale-free topology. However, the underlying premise that biological networks are scale-free is contentious.[14][15][16]

lmQCM is an alternative for WGCNA achieving the same goal of gene co-expression networks analysis. lmQCM,[17] stands for local maximal Quasi-Clique Merger, aiming to exploit the locally dense structures in the network, thus can mine smaller and densely co-expressed modules by allowing module overlapping. the algorithm lmQCM has its R package and python module (bundled in Biolearns). The generally smaller size of mined modules can also generate more meaningful gene ontology (GO) enrichment results.

Challenges

Co-expression networks try to estimate the direct and sometimes the indirect correlations between pairs of genes. However, an individual gene may be controlled by multiple regulators.[18] Second, as discussed in the previous sections, each co-expression computational measure is designed specifically to capture a unique feature that is not necessarily optimal for depicting all types of gene-to-gene transcriptional inter-relation, for example, Pearson correlation for linear relations, Spearman for the ranking of the genes, and so on. Third and last, calculating the gene to gene co-expression networks for whole genome results in very large matrices which contain a considerable amount of noise, which raises a significant difficulty in exploring their differentiation across cohorts. These challenges should be referred when applying advanced methods of co-expression on gene expression data.

Applications
  • Single cell sequencing - Gene co-expression networks generated using bulk RNA-Seq data have been used to boost the signal/noise ratio in single cell scenarios, in order to obtain better predictions of the presence of specific mutations in single cell, using gene expression profiles as independent variables[19]
  • Gene Network Reverse Engineering - Hundreds of methods to infer gene regulatory networks exists, and several dozens are currently based on co-expression analysis, based on simple correlation, mutual information or bayesian methods.[20]
  • Plant Biology - Co-expression analyses have been extensively used to search for novel genes involved in specific plant pathways. One example is cell wall synthesis: the characterization of missing links in this metabolic mechanism was made possible by finding new Cellulose Synthase genes (CESAs), whose expression profiles are correlating with previously known pathway members.[21]

See also

References
  1. Stuart, Joshua M; Segal, Eran; Koller, Daphne; Kim, Stuart K (2003). "A gene-coexpression network for global discovery of conserved genetic modules". Science. 302 (5643): 249–55. Bibcode:2003Sci...302..249S. CiteSeerX 10.1.1.119.6331. doi:10.1126/science.1087447. PMID 12934013. S2CID 3131371.
  2. Weirauch, Matthew T (2011). "Gene coexpression networks for the analysis of DNA microarray data". Applied Statistics for Network Biology: Methods in Systems Biology. pp. 215–250. doi:10.1002/9783527638079.ch11. ISBN 9783527638079.
  3. Roy, Swarup; Bhattacharyya, Dhruba K; Kalita, Jugal K (2014). "Reconstruction of gene co-expression network from microarray data using local expression patterns". BMC Bioinformatics. 15: S10. doi:10.1186/1471-2105-15-s7-s10. PMC 4110735. PMID 25079873.
  4. De Smet, Riet; Marchal, Kathleen (2010). "Advantages and limitations of current network inference methods". Nature Reviews Microbiology. 8 (10): 717–29. doi:10.1038/nrmicro2419. PMID 20805835. S2CID 27629033.
  5. Butte, Atul J; Kohane, Isaac S (1999). "Unsupervised knowledge discovery in medical databases using relevance networks". Proceedings of the AMIA Symposium.
  6. Butte, Atul J; Kohane, Isaac S (2000). "Mutual information relevance networks: functional genomic clustering using pairwise entropy measurements". Pac Symp Biocomput. 5.
  7. Villa-Vialaneix, Nathalie; Liaubet, Laurence; Laurent, Thibault; Cherel, Pierre; Gamot, Adrien; SanCristobal, Magali (2013). "The structure of a gene co-expression network reveals biological functions underlying eQTLs". PLOS ONE. 8 (4): 60045. Bibcode:2013PLoSO...860045V. doi:10.1371/journal.pone.0060045. PMC 3618335. PMID 23577081.
  8. Persson, Staffan; Wei, Hairong; Milne, Jennifer; Page, Grier P; Somerville, Christopher R (2005). "Identification of genes required for cellulose synthesis by regression analysis of public microarray data sets". Proceedings of the National Academy of Sciences of the United States of America. 102 (24): 8633–8. Bibcode:2005PNAS..102.8633P. doi:10.1073/pnas.0503392102. PMC 1142401. PMID 15932943.
  9. Reverter, Antonio; Chan, Eva KF (2008). "Combining partial correlation and an information theory approach to the reversed engineering of gene co-expression networks". Bioinformatics. 24 (21): 2491–2497. doi:10.1093/bioinformatics/btn482. PMID 18784117.
  10. Song, Lin; Langfelder, Peter; Horvath, Steve (2012). "Comparison of co-expression measures: mutual information, correlation, and model based indices". BMC Bioinformatics. 13 (1): 328. doi:10.1186/1471-2105-13-328. PMC 3586947. PMID 23217028.
  11. Elo, Laura L; Järvenpää, Henna; Orešič, Matej; Lahesmaa, Riitta; Aittokallio, Tero (2007). "Systematic construction of gene coexpression networks with applications to human T helper cell differentiation process". Bioinformatics. 23 (16): 2096–2103. doi:10.1093/bioinformatics/btm309. PMID 17553854.
  12. Luo, Feng; Yang, Yunfeng; Zhong, Jianxin; Gao, Haichun; Khan, Latifur; Thompson, Dorothea K; Zhou, Jizhong (2007). "Constructing gene co-expression networks and predicting functions of unknown genes by random matrix theory". BMC Bioinformatics. 8 (1): 299. doi:10.1186/1471-2105-8-299. PMC 2212665. PMID 17697349.
  13. Zhang, Bin; Horvath, Steve (2005). "A general framework for weighted gene co-expression network analysis". Statistical Applications in Genetics and Molecular Biology. 4 (1): Article17. CiteSeerX 10.1.1.471.9599. doi:10.2202/1544-6115.1128. PMID 16646834. S2CID 7756201.
  14. Khanin, R.; Wit, E. (2006). "How scale-free are biological networks". Journal of Computational Biology. 13 (3): 810–8. doi:10.1089/cmb.2006.13.810. PMID 16706727.
  15. Broido, Anna D.; Clauset, Aaron (2019). "Scale-free networks are rare". Nature Communications. 10 (1): 1017. arXiv:1801.03400. Bibcode:2019NatCo..10.1017B. doi:10.1038/s41467-019-08746-5. PMC 6399239. PMID 30833554. S2CID 24825063.
  16. Clote, P. (2020). "Are RNA networks scale-free?". Journal of Mathematical Biology. 80 (5): 1291–1321. doi:10.1007/s00285-019-01463-z. PMC 7052049. PMID 31950258.
  17. Zhang, Jie; Huang, Kun (2014). "Normalized ImQCM: An Algorithm for Detecting Weak Quasi-Cliques in Weighted Graph with Applications in Gene Co-Expression Module Discovery in Cancers". Cancer Informatics. 13 (3): 137–46. doi:10.4137/CIN.S14021. PMC 4962959. PMID 27486298.
  18. Alon, Uri. ": Design Principles of Biological Circuits". doi:10.1201/9781420011432.
  19. Mercatelli, Daniele; Ray, Forest; Giorgi, Federico M. (2019). "Pan-Cancer and Single-Cell Modeling of Genomic Alterations Through Gene Expression". Frontiers in Genetics. 10: 671. doi:10.3389/fgene.2019.00671. ISSN 1664-8021. PMC 6657420. PMID 31379928.
  20. Mercatelli, Daniele; Scalambra, Laura; Triboli, Luca; Ray, Forest; Giorgi, Federico M. (2020). "Gene regulatory network inference resources: A practical overview". Biochimica et Biophysica Acta (BBA) - Gene Regulatory Mechanisms. 1863 (6): 194430. doi:10.1016/j.bbagrm.2019.194430. ISSN 1874-9399. PMID 31678629. S2CID 207895066.
  21. Usadel, Bjoern; Obayashi, Takeshi; Mutwil, Marek; Giorgi, Federico M.; Bassel, George W.; Tanimoto, Mimi; Chow, Amanda; Steinhauser, Dirk; Persson, Staffan; Provart, Nicholas J. (2009). "Co-expression tools for plant biology: opportunities for hypothesis generation and caveats". Plant, Cell & Environment. 32 (12): 1633–1651. doi:10.1111/j.1365-3040.2009.02040.x. ISSN 0140-7791. PMID 19712066.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.