Grandsire

The "plain course" of Grandsire Doubles; 30 changes[1]

Showing the effects of bobs and singles

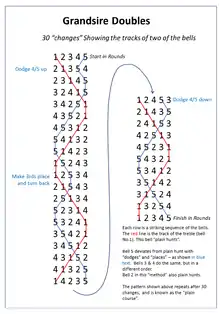
Grandsire, like Plain Bob, is based on a simple deviation to the plain hunt when the treble (bell No.1) is first in the sequence or it is said to "lead". The treble is known as the "hunt bell" because it hunts continuously without ever deviating from the path. The diagram for the plain course is shown here.[2]

The Grandsire variation on the plain hunt on odd numbers adds a second hunt bell, which is "coursing" the treble: that is, the second hunt bell takes its place at the front of the change immediately after the treble. The single deviation away from hunting for the rest of the bells now takes place as the two hunt bells change places at the front of the lead.

Furthermore, because there are two hunt bells, not the second bell but the third remains in place:

13254 – Treble leads
12345
21354 – The second hunt bell, No.2 in this case, leads after the treble. It is coursing it. 
23145

This forces a dodge on the other bells in 4/5 positions. After this the bells immediately return to the plain hunt pattern until the next treble lead.[3]

This rule can now be extended to any number of odd bells in changes, making Grandsire an easily extendable method. The hunt bell is changed many times during such ringing to enable the full factorial number of changes to be achieved.[4]

The plain course of Grandsire Doubles is shown, but it extends only to 30 different rows or changes. To extend to 120 rows, which is the maximum number of different rows possible on five bells, the "calls" known as Bobs and Singles are used. These are referred to as "calls", because they are called by the "conductor" according to a "composition" which has been memorised.[5] The calls are made when the treble is in 3rds place approaching the lead,. A typical composition shown by the sequential treble leads to get 120 changes is: Plain, Bob, Plain, Bob, Plain, Single; repeated once. "Plain" means there is no call. There are 10 different compositions which can achieve this.[6]

Grandsire is usually an odd-bell method and the following suffixes are used to describe it when the changes are rung on different numbers of bells. There is a normally a cover bell ringing in last place at each row, to add musicality and rhythm, but Grandsire may be rung without a cover.

The method was devised around 1650, probably by Robert Roan who became master of the College Youths change ringing society in 1652.[7] Details of the method on five bells appeared in print in 1668 in Tintinnalogia, the first book to be published on change ringing. By this time, Roan had invented a six-bell extension he named "Grandsire Bob", now known by ringers as "Plain Bob Minor". The description of Grandsire predates modern method naming conventions. Grandsire on an odd numbers of bells (as it is usually rung) would share a name with the method known as "plain bob" on even numbers of bells in modern nomenclature. However, Grandsire Bob is a method separate from plain bob by having the 4-5 dodges and thirds of Grandsire doubles, but with long sixths at the back (plain bob doubles have long fifths).

It was found the 120 possible changes of doubles could only be rung by the introduction at some point of "single" changes – that is, changes in which only two bells change position. Only two such singles were required. Historically, it was unclear whether the 5040 (7! = factorial 7 = 7×6×5×4×3×2×1) possible changes of triples required a similar compromise. Although attempts at triples compositions appeared in print as early as 1702, and a peal composed by John Garthon was rung in 1718, it was 1751 before John Holt produced the first satisfactory peal composition.

William Henry Thompson, a mathematician, proved in a paper published in 1880 that it was impossible to achieve the 5040 changes using the normal bobs only, without the use of singles or some other type of call. This result had long been suspected by peal composers, but it had not been proved.[8] Peal length round blocks of caters and cinques were more easily achieved. However, the ringing of Grandsire at these stages was limited by the relative rarity of towers with sufficient bells, and Grandsire Caters was first rung to a peal length in 1717 and Grandsire Cinques in 1725.

Grandsire at all stages is still frequently rung today. It is often one of the first methods learnt by new bell ringers. According to the best available knowledge in 2017, 6,929 peals of Grandsire Caters (on 10 bells) were rung in the 300 years after 11 January 1711. Grandsire Caters was the leading 10-bell method in each decade from 1711 to 1890, but Stedman Caters has proved more popular recently and on 9 July 2010 its cumulative peal total from 1711 pulled ahead of the running Grandsire total.[9]

• Trollope, J. Armiger (1948). Grandsire, Jasper Snowdon Change Ringing Series. Reprint 1973: Christopher Groome, Burton Latimer.
• Richard Duckworth and Fabian Stedman (1671). Tintinnalogia, or, the Art of Ringing at Project Gutenberg

• J. Monk (1766). "Grandsire Triples". Campanalogia Improved: Or, The Art of Ringing Made Easy, by Plain and Methodical Rules and Directions. London: L. Hawes, W. Clarke, and R. Collins; and S. Crowder. pp. 117–137.

• Graphical representation of the pattern on five bells