Functional square root

Notations expressing that f is a functional square root of g are f = g_[1/2] and f = g_1/2.

• The functional square root of the exponential function (now known as a half-exponential function) was studied by Hellmuth Kneser in 1950.[1]
• The solutions of f(f(x)) = x over ${\displaystyle \mathbb {R} }$ (the involutions of the real numbers) were first studied by Charles Babbage in 1815, and this equation is called Babbage's functional equation.[2] A particular solution is f(x) = (b − x)/(1 + cx) for bc ≠ −1. Babbage noted that for any given solution f, its functional conjugate Ψ⁻¹∘ f ∘ Ψ by an arbitrary invertible function Ψ is also a solution. In other words, the group of all invertible functions on the real line acts on the subset consisting of solutions to Babbage's functional equation by conjugation.

A systematic procedure to produce arbitrary functional n-roots (including arbitrary real, negative, and infinitesimal n) of functions ${\displaystyle g:\mathbb {C} \rightarrow \mathbb {C} }$ relies on the solutions of Schröder's equation.[3][4][5] Infinitely many trivial solutions exist when the domain of a root function f is allowed to be sufficiently larger than that of g.

• f(x) = 2x² is a functional square root of g(x) = 8x⁴.
• A functional square root of the nth Chebyshev polynomial, g(x) = T_n(x), is f(x) = cos(√n arccos(x)), which in general is not a polynomial.
• f(x) = x/(√2 + x(1 − √2)) is a functional square root of g(x) = x/(2 − x).

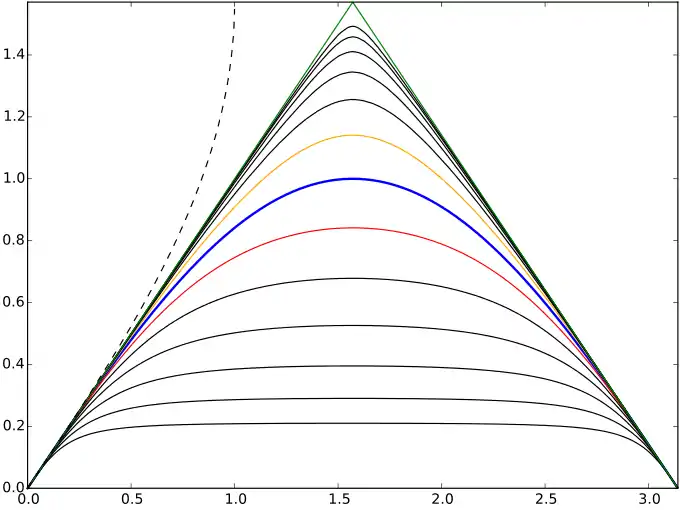
Iterates of the sine function (blue), in the first half-period. Half-iterate (orange), i.e., the sine's functional square root; the functional square root of that, the quarter-iterate (black) above it, and further fractional iterates up to the 1/64th iterate. The functions below sine are six integral iterates below it, starting with the second iterate (red) and ending with the 64th iterate. The green envelope triangle represents the limiting null iterate, the sawtooth function serving as the starting point leading to the sine function. The dashed line is the negative first iterate, i.e. the inverse of sine (arcsin).

sin_[2](x) = sin(sin(x)) [red curve]

sin_[1](x) = sin(x) = rin(rin(x)) [blue curve]

sin_[1/2](x) = rin(x) = qin(qin(x)) [orange curve]

sin_[1/4](x) = qin(x) [black curve above the orange curve]

sin_[–1](x) = arcsin(x) [dashed curve]

(See.[6] For the notation, see .)