Half-side formula

In spherical trigonometry, the half side formula relates the angles and lengths of the sides of spherical triangles, which are triangles drawn on the surface of a sphere and so have curved sides and do not obey the formulas for plane triangles.[1]

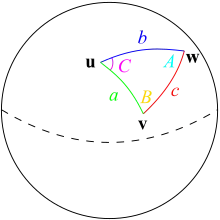
Spherical triangle

Formulas

For a triangle on a sphere with radius $r$ , the half-side formulas are[2]

{\begin{aligned}\tan \left({\frac {a}{2r}}\right)&=R\cos(S-A)\\\tan \left({\frac {b}{2r}}\right)&=R\cos(S-B)\\\tan \left({\frac {c}{2r}}\right)&=R\cos(S-C)\end{aligned}}

where

$a$ , $b$ , and $c$ are the lengths of the sides respectively opposite angles $A$ , $B$ , and $C$ ;
$S={\frac {1}{2}}(A+B+C)$ is half the sum of the angles; and
$R={\sqrt {\frac {-\cos S}{\cos(S-A)\cos(S-B)\cos(S-C)}}}.$

The three formulas are really the same formula, with the names of the variables permuted.

The sides $a$ , $b$ , and $c$ are normalized by the $1/ r$ factor so that they represent arc lengths on a unit sphere.

References

Bronshtein, I. N.; Semendyayev, K. A.; Musiol, Gerhard; Mühlig, Heiner (2007), Handbook of Mathematics, Springer, p. 165, ISBN 9783540721222
Nelson, David (2008), The Penguin Dictionary of Mathematics (4th ed.), Penguin UK, p. 529, ISBN 9780141920870.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Bronshtein, I. N.; Semendyayev, K. A.; Musiol, Gerhard; Mühlig, Heiner (2007), Handbook of Mathematics, Springer, p. 165, ISBN 9783540721222

[2] Nelson, David (2008), The Penguin Dictionary of Mathematics (4th ed.), Penguin UK, p. 529, ISBN 9780141920870.

Half-side formula

Formulas

See also

References