Half-precision floating-point format

In computing, half precision (sometimes called FP16 or float16) is a binary floating-point computer number format that occupies 16 bits (two bytes in modern computers) in computer memory. It is intended for storage of floating-point values in applications where higher precision is not essential, in particular image processing and neural networks.

Not to be confused with bfloat16, a different 16-bit floating-point format.

Almost all modern uses follow the IEEE 754-2008 standard, where the 16-bit base-2 format is referred to as binary16, and the exponent uses 5 bits. This can express values in the range ±65,504, with the minimum value above 1 being 1 + 1/1024.

Depending on the computer, half-precision can be over an order of magnitude faster than double precision, e.g. 550 PFLOPS for half-precision vs 37 PFLOPS for double precision on one cloud provider.[1]

Floating-point formats
IEEE 754
Other

History

Several earlier 16-bit floating point formats have existed including that of Hitachi's HD61810 DSP of 1982 (a 4-bit exponent and a 12-bit mantissa),[2] Thomas J. Scott's WIF of 1991 (5 exponent bits, 10 mantissa bits)[3] and the 3dfx Voodoo Graphics processor of 1995 (same as Hitachi).[4]

ILM was searching for an image format that could handle a wide dynamic range, but without the hard drive and memory cost of single or double precision floating point.[5] The hardware-accelerated programmable shading group led by John Airey at SGI (Silicon Graphics) invented the s10e5 data type in 1997 as part of the 'bali' design effort. This is described in a SIGGRAPH 2000 paper[6] (see section 4.3) and further documented in US patent 7518615.[7] It was popularized by its use in the open-source OpenEXR image format.

Nvidia and Microsoft defined the half datatype in the Cg language, released in early 2002, and implemented it in silicon in the GeForce FX, released in late 2002.[8] Since then support for 16-bit floating point math in graphics cards has become very common.

The F16C extension in 2012 allows x86 processors to convert half-precision floats to and from single-precision floats with a machine instruction.

IEEE 754 half-precision binary floating-point format: binary16

The IEEE 754 standard[9] specifies a binary16 as having the following format:

The format is laid out as follows:

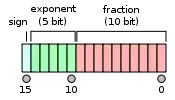
The format is assumed to have an implicit lead bit with value 1 unless the exponent field is stored with all zeros. Thus, only 10 bits of the significand appear in the memory format but the total precision is 11 bits. In IEEE 754 parlance, there are 10 bits of significand, but there are 11 bits of significand precision (log10(211) ≈ 3.311 decimal digits, or 4 digits ± slightly less than 5 units in the last place).

Exponent encoding

The half-precision binary floating-point exponent is encoded using an offset-binary representation, with the zero offset being 15; also known as exponent bias in the IEEE 754 standard.[9]

  • Emin = 000012 − 011112 = −14
  • Emax = 111102 − 011112 = 15
  • Exponent bias = 011112 = 15

Thus, as defined by the offset binary representation, in order to get the true exponent the offset of 15 has to be subtracted from the stored exponent.

The stored exponents 000002 and 111112 are interpreted specially.

ExponentSignificand = zeroSignificand ≠ zeroEquation
000002zero, −0subnormal numbers(−1)signbit × 2−14 × 0.significantbits2
000012, ..., 111102normalized value(−1)signbit × 2exponent−15 × 1.significantbits2
111112±infinityNaN (quiet, signalling)

The minimum strictly positive (subnormal) value is 2−24 ≈ 5.96 × 10−8. The minimum positive normal value is 2−14 ≈ 6.10 × 10−5. The maximum representable value is (2−2−10) × 215 = 65504.

Half precision examples

These examples are given in bit representation of the floating-point value. This includes the sign bit, (biased) exponent, and significand.

BinaryHexValueNotes
0 00000 000000000000000
0 00000 000000000100012−14 × (0 + 1/1024 ) ≈ 0.000000059604645smallest positive subnormal number
0 00000 111111111103ff2−14 × (0 + 1023/1024 ) ≈ 0.000060975552largest subnormal number
0 00001 000000000004002−14 × (1 + 0/1024 ) ≈ 0.00006103515625smallest positive normal number
0 01101 010101010135552−2 × (1 + 341/1024 ) ≈ 0.33325195nearest value to 1/3
0 01110 11111111113bff2−1 × (1 + 1023/1024 ) ≈ 0.99951172largest number less than one
0 01111 00000000003c0020 × (1 + 0/1024 ) = 1one
0 01111 00000000013c0120 × (1 + 1/1024 ) ≈ 1.00097656smallest number larger than one
0 11110 11111111117bff215 × (1 + 1023/1024 ) = 65504largest normal number
0 11111 00000000007c00∞infinity
1 00000 00000000008000−0
1 10000 0000000000c000−2
1 11111 0000000000fc00−∞negative infinity

By default, 1/3 rounds down like for double precision, because of the odd number of bits in the significand. The bits beyond the rounding point are 0101... which is less than 1/2 of a unit in the last place.

Precision limitations
MinMaxinterval
02−132−24
2−132−122−23
2−122−112−22
2−112−102−21
2−102−92−20
2−92−82−19
2−82−72−18
2−72−62−17
2−62−52−16
2−52−42−15
2−41/82−14
1/81/42−13
1/41/22−12
1/212−11
122−10
242−9
482−8
8162−7
16322−6
32642−5
641282−4
1282561/8
2565121/4
51210241/2
102420481
204840962
409681924
8192163848
163843276816
327686551932
65519∞∞

65519 is the largest number that will round to a finite number (65504), 65520 and larger will round to infinity. This is for round-to-even, other rounding strategies will change this cut-off.

ARM alternative half-precision

ARM processors support (via a floating point control register bit) an "alternative half-precision" format, which does away with the special case for an exponent value of 31 (111112).[10] It is almost identical to the IEEE format, but there is no encoding for infinity or NaNs; instead, an exponent of 31 encodes normalized numbers in the range 65536 to 131008.

Uses of half precision

Half precision is used in several computer graphics environments to store pixels, including MATLAB, OpenEXR, JPEG XR, GIMP, OpenGL, Vulkan,[11] Cg, Direct3D, and D3DX. The advantage over 8-bit or 16-bit integers is that the increased dynamic range allows for more detail to be preserved in highlights and shadows for images, and the linear representation of intensity making calculations easier. The advantage over 32-bit single-precision floating point is that it requires half the storage and bandwidth (at the expense of precision and range).[5]

Half precision can be useful for mesh quantization. Mesh data is usually stored using 32-bit single precision floats for the vertices, however in some situations it is acceptable to reduce the precision to only 16-bit half precision, requiring only half the storage at the expense of some precision. Mesh quantization can also be done with 8-bit or 16-bit fixed precision depending on the requirements.[12]

Hardware and software for machine learning or neural networks tend to use half precision: such applications usually do a large amount of calculation, but don't require a high level of precision. Due to hardware typically not supporting 16-bit half precision floats, neural networks often use the bfloat16 format, which is the single precision float format truncated to 16 bits.

If the hardware has instructions to compute half-precision math, it is often faster than single or double precision. If the systems has SIMD instructions that can handle multiple floating-point numbers within one instruction, half precision can be twice as fast by operating on twice as many numbers simultaneously.[13]

Hardware support

Several versions of the ARM architecture have support for half precision.[14]

Support for half precision in the x86 instruction set is specified in the F16C instruction set extension, first introduced in 2009 by AMD and fairly broadly adopted by AMD and Intel CPUs by 2012. This was further extended up the AVX-512_FP16 instruction set extension implemented in the Intel Sapphire Rapids processor.[15]

On RISC-V, the Zfh and Zfhmin extensions provide hardware support for 16-bit half precision floats. The Zfhmin extension is a minimal alternative to Zfh.[16]

On Power ISA, VSX and the not-yet-approved SVP64 extension provide hardware support for 16-bit half precision floats as of PowerISA v3.1B and later.[17][18]

See also

References
  1. "About ABCI - About ABCI | ABCI". abci.ai. Retrieved 2019-10-06.
  2. "hitachi :: dataBooks :: HD61810 Digital Signal Processor Users Manual". Archive.org. Retrieved 2017-07-14.
  3. Scott, Thomas J. (March 1991). "Mathematics and computer science at odds over real numbers". Proceedings of the twenty-second SIGCSE technical symposium on Computer science education - SIGCSE '91. Vol. 23. pp. 130–139. doi:10.1145/107004.107029. ISBN 0897913779. S2CID 16648394.
  4. "/home/usr/bk/glide/docs2.3.1/GLIDEPGM.DOC". Gamers.org. Retrieved 2017-07-14.
  5. "OpenEXR". OpenEXR. Retrieved 2017-07-14.
  6. Mark S. Peercy; Marc Olano; John Airey; P. Jeffrey Ungar. "Interactive Multi-Pass Programmable Shading" (PDF). People.csail.mit.edu. Retrieved 2017-07-14.
  7. "Patent US7518615 - Display system having floating point rasterization and floating point ... - Google Patents". Google.com. Retrieved 2017-07-14.
  8. "vs_2_sw". Cg 3.1 Toolkit Documentation. Nvidia. Retrieved 17 August 2016.
  9. IEEE Standard for Floating-Point Arithmetic. IEEE STD 754-2019 (Revision of IEEE 754-2008). July 2019. pp. 1–84. doi:10.1109/ieeestd.2019.8766229. ISBN 978-1-5044-5924-2.
  10. "Half-precision floating-point number support". RealView Compilation Tools Compiler User Guide. 10 December 2010. Retrieved 2015-05-05.
  11. Garrard, Andrew. "10.1. 16-bit floating-point numbers". Khronos Data Format Specification v1.2 rev 1. Khronos. Retrieved 2023-08-05.
  12. "KHR_mesh_quantization". GitHub. Khronos Group. Retrieved 2023-07-02.
  13. Ho, Nhut-Minh; Wong, Weng-Fai (September 1, 2017). "Exploiting half precision arithmetic in Nvidia GPUs" (PDF). Department of Computer Science, National University of Singapore. Retrieved July 13, 2020. Nvidia recently introduced native half precision floating point support (FP16) into their Pascal GPUs. This was mainly motivated by the possibility that this will speed up data intensive and error tolerant applications in GPUs.
  14. "Half-precision floating-point number format". ARM Compiler armclang Reference Guide Version 6.7. ARM Developer. Retrieved 13 May 2022.
  15. Towner, Daniel. "Intel® Advanced Vector Extensions 512 - FP16 Instruction Set for Intel® Xeon® Processor Based Products" (PDF). Intel® Builders Programs. Retrieved 13 May 2022.
  16. "RISC-V Instruction Set Manual, Volume I: RISC-V User-Level ISA". Five EmbedDev. Retrieved 2023-07-02.
  17. "OPF_PowerISA_v3.1B.pdf". OpenPOWER Files. OpenPOWER Foundation. Retrieved 2023-07-02.
  18. "ls005.xlen.mdwn". libre-soc.org Git. Retrieved 2023-07-02.

Further reading
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.