Hering–Hillebrand deviation
The Hering–Hillebrand deviation describes the mismatch between the theoretical and empirical horopter. The horopter is the set of points that projects at the same location in the two retinae (i.e. that have the same visual direction). Geometrically the horopter is a circle passing through the nodal point of the two eyes and through the fixation point. This is known as the horizontal geometrical horopter, or as the Vieth–Müller circle. This is the set of points that correspond geometrically to the intersection between visual lines at identical eccentricities. There is also a vertical horopter which is a straight line on the sagittal plane and passing through the intersection between the sagittal plane and the Vieth–Müller circle (typically fixation if the observer fixates straight ahead, but not necessarily).[1][2]
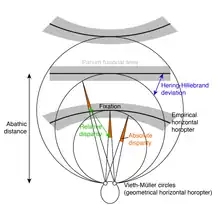
An empirical horopter can be defined following different criteria. Following Hering,[3] it is usually meant by empirical horopter the equal visual direction horopter. That is the set of points that appear to have the same visual direction in both eyes. But the horopter can also be defined as the center of the Panum's fusional area, the apparent fronto-parallel plane or the equal distance from fixation. All these empirical horopters are in fact corresponding, empirically, to the equal visual direction horopter.
The Hering–Hillebrand deviation describes the fact that the empirical horopter does not fall on the geometrical horopter. This was observed by Hering and Hillebrand at the same time, as well as Helmholtz for the vertical horopter.[4] At short fixation distances, the empirical horopter is a concave parabola flatter that a circle. At some given distance, called the abathic distance, the empirical horopter becomes a straight line, thus matching the apparent fronto-parallel plane. Finally for fixation distances farther than the abathic distance the empirical horopter is a convex parabola.
The origin of the Hering–Hilebrand deviation is still unclear. It was originally thought to reflect a compromise between the Vieth–Müller circle and fronto-parallel plane. But this is true only for short fixation distances where the empirical horopter is intermediate between these two set of points. More recently natural images analyses suggested that the shape of the empirical horopter might match natural images statistics.[5]
See also
Notes
- Howard, Ian P; Rogers, Brian J (2002). Seeing in depth, volume 2: Depth perception. Ontario, Canada: I. Porteous.
- Tyler, Christopher W (1991). The horopter and binocular fusion. In Vision and visual dysfunction 9. pp. 19–37.
- Hering, Ewald (1977). Stark, Lawrence; Bridgeman, Bruce (eds.). The theory of binocular vision. Bridgeman, Bruce. New York: Plenum Press. ISBN 0-306-31016-3.
- von Helmholtz, Hermann (1924). Treatise on physiological optics (Vol. 3). The Optical Society of America.
- Sprague, William W; Cooper, Emily A; Tošić, Ivana; Banks, Martin S (2015). "Stereopsis is adaptive for the natural environment". Science Advances. 1 (4): e1400254. doi:10.1126/sciadv.1400254. PMC 4507831. PMID 26207262.