Hermite polynomials
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence.
The polynomials arise in:
- signal processing as Hermitian wavelets for wavelet transform analysis
- probability, such as the Edgeworth series, as well as in connection with Brownian motion;
- combinatorics, as an example of an Appell sequence, obeying the umbral calculus;
- numerical analysis as Gaussian quadrature;
- physics, where they give rise to the eigenstates of the quantum harmonic oscillator; and they also occur in some cases of the heat equation (when the term is present);
- systems theory in connection with nonlinear operations on Gaussian noise.
- random matrix theory in Gaussian ensembles.
Hermite polynomials were defined by Pierre-Simon Laplace in 1810,[1][2] though in scarcely recognizable form, and studied in detail by Pafnuty Chebyshev in 1859.[3] Chebyshev's work was overlooked, and they were named later after Charles Hermite, who wrote on the polynomials in 1864, describing them as new.[4] They were consequently not new, although Hermite was the first to define the multidimensional polynomials in his later 1865 publications.
Definition
Like the other classical orthogonal polynomials, the Hermite polynomials can be defined from several different starting points. Noting from the outset that there are two different standardizations in common use, one convenient method is as follows:
- The "probabilist's Hermite polynomials" are given by
- while the "physicist's Hermite polynomials" are given by
These equations have the form of a Rodrigues' formula and can also be written as,
The two definitions are not exactly identical; each is a rescaling of the other:
These are Hermite polynomial sequences of different variances; see the material on variances below.
The notation He and H is that used in the standard references.[5] The polynomials Hen are sometimes denoted by Hn, especially in probability theory, because
is the probability density function for the normal distribution with expected value 0 and standard deviation 1.
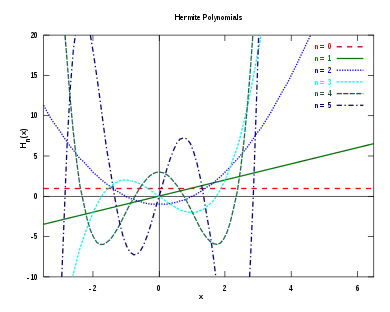
- The first eleven probabilist's Hermite polynomials are:
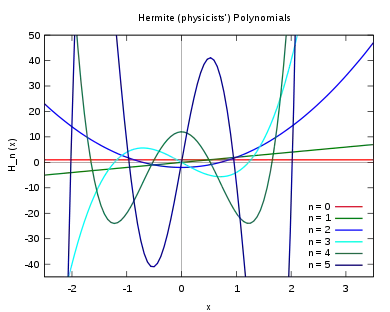
- The first eleven physicist's Hermite polynomials are:
Properties
The nth-order Hermite polynomial is a polynomial of degree n. The probabilist's version Hen has leading coefficient 1, while the physicist's version Hn has leading coefficient 2n.
Symmetry
From the Rodrigues formulae given above, we can see that Hn(x) and Hen(x) are even or odd functions depending on n:
Orthogonality
Hn(x) and Hen(x) are nth-degree polynomials for n = 0, 1, 2, 3,.... These polynomials are orthogonal with respect to the weight function (measure)
or
i.e., we have
Furthermore,
or
where is the Kronecker delta.
The probabilist polynomials are thus orthogonal with respect to the standard normal probability density function.
Completeness
The Hermite polynomials (probabilist's or physicist's) form an orthogonal basis of the Hilbert space of functions satisfying
in which the inner product is given by the integral
including the Gaussian weight function w(x) defined in the preceding section
An orthogonal basis for L2(R, w(x) dx) is a complete orthogonal system. For an orthogonal system, completeness is equivalent to the fact that the 0 function is the only function f ∈ L2(R, w(x) dx) orthogonal to all functions in the system.
Since the linear span of Hermite polynomials is the space of all polynomials, one has to show (in physicist case) that if f satisfies
for every n ≥ 0, then f = 0.
One possible way to do this is to appreciate that the entire function
vanishes identically. The fact then that F(it) = 0 for every real t means that the Fourier transform of f(x)e−x2 is 0, hence f is 0 almost everywhere. Variants of the above completeness proof apply to other weights with exponential decay.
In the Hermite case, it is also possible to prove an explicit identity that implies completeness (see section on the Completeness relation below).
An equivalent formulation of the fact that Hermite polynomials are an orthogonal basis for L2(R, w(x) dx) consists in introducing Hermite functions (see below), and in saying that the Hermite functions are an orthonormal basis for L2(R).
Hermite's differential equation
The probabilist's Hermite polynomials are solutions of the differential equation
where λ is a constant. Imposing the boundary condition that u should be polynomially bounded at infinity, the equation has solutions only if λ is a non-negative integer, and the solution is uniquely given by , where denotes a constant.
Rewriting the differential equation as an eigenvalue problem
the Hermite polynomials may be understood as eigenfunctions of the differential operator . This eigenvalue problem is called the Hermite equation, although the term is also used for the closely related equation
whose solution is uniquely given in terms of physicist's Hermite polynomials in the form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/en.wikipedia.org/v1/":): {\displaystyle u(x) = C_1 H_\lambda(x) } , where denotes a constant, after imposing the boundary condition that u should be polynomially bounded at infinity.
The general solutions to the above second-order differential equations are in fact linear combinations of both Hermite polynomials and confluent hypergeometric functions of the first kind. For example, for the physicist's Hermite equation
the general solution takes the form
where and are constants, are physicist's Hermite polynomials (of the first kind), and are physicist's Hermite functions (of the second kind). The latter functions are compactly represented as where are Confluent hypergeometric functions of the first kind. The conventional Hermite polynomials may also be expressed in terms of confluent hypergeometric functions, see below.
With more general boundary conditions, the Hermite polynomials can be generalized to obtain more general analytic functions for complex-valued λ. An explicit formula of Hermite polynomials in terms of contour integrals (Courant & Hilbert 1989) is also possible.
Recurrence relation
The sequence of probabilist's Hermite polynomials also satisfies the recurrence relation
Individual coefficients are related by the following recursion formula:
and a0,0 = 1, a1,0 = 0, a1,1 = 1.
For the physicist's polynomials, assuming
we have
Individual coefficients are related by the following recursion formula:
and a0,0 = 1, a1,0 = 0, a1,1 = 2.
The Hermite polynomials constitute an Appell sequence, i.e., they are a polynomial sequence satisfying the identity
Equivalently, by Taylor-expanding,
These umbral identities are self-evident and included in the differential operator representation detailed below,
In consequence, for the mth derivatives the following relations hold:
It follows that the Hermite polynomials also satisfy the recurrence relation
These last relations, together with the initial polynomials H0(x) and H1(x), can be used in practice to compute the polynomials quickly.
Moreover, the following multiplication theorem holds:
Explicit expression
The physicist's Hermite polynomials can be written explicitly as
These two equations may be combined into one using the floor function:
The probabilist's Hermite polynomials He have similar formulas, which may be obtained from these by replacing the power of 2x with the corresponding power of √2 x and multiplying the entire sum by 2−n/2:
Inverse explicit expression
The inverse of the above explicit expressions, that is, those for monomials in terms of probabilist's Hermite polynomials He are
The corresponding expressions for the physicist's Hermite polynomials H follow directly by properly scaling this:[6]
Generating function
The Hermite polynomials are given by the exponential generating function
This equality is valid for all complex values of x and t, and can be obtained by writing the Taylor expansion at x of the entire function z → e−z2 (in the physicist's case). One can also derive the (physicist's) generating function by using Cauchy's integral formula to write the Hermite polynomials as
Using this in the sum
one can evaluate the remaining integral using the calculus of residues and arrive at the desired generating function.
Expected values
If X is a random variable with a normal distribution with standard deviation 1 and expected value μ, then
The moments of the standard normal (with expected value zero) may be read off directly from the relation for even indices:
where (2n − 1)!! is the double factorial. Note that the above expression is a special case of the representation of the probabilist's Hermite polynomials as moments:
Asymptotic expansion
Asymptotically, as n → ∞, the expansion[7]
holds true. For certain cases concerning a wider range of evaluation, it is necessary to include a factor for changing amplitude:
which, using Stirling's approximation, can be further simplified, in the limit, to
This expansion is needed to resolve the wavefunction of a quantum harmonic oscillator such that it agrees with the classical approximation in the limit of the correspondence principle.
A better approximation, which accounts for the variation in frequency, is given by
A finer approximation,[8] which takes into account the uneven spacing of the zeros near the edges, makes use of the substitution
with which one has the uniform approximation
Similar approximations hold for the monotonic and transition regions. Specifically, if
then
while for
with t complex and bounded, the approximation is
where Ai is the Airy function of the first kind.
Special values
The physicist's Hermite polynomials evaluated at zero argument Hn(0) are called Hermite numbers.
which satisfy the recursion relation Hn(0) = −2(n − 1)Hn − 2(0).
In terms of the probabilist's polynomials this translates to
Relations to other functions
Laguerre polynomials
The Hermite polynomials can be expressed as a special case of the Laguerre polynomials:
Relation to confluent hypergeometric functions
The physicist's Hermite polynomials can be expressed as a special case of the parabolic cylinder functions:
in the right half-plane, where U(a, b, z) is Tricomi's confluent hypergeometric function. Similarly,
where 1F1(a, b; z) = M(a, b; z) is Kummer's confluent hypergeometric function.
Differential-operator representation
The probabilist's Hermite polynomials satisfy the identity
where D represents differentiation with respect to x, and the exponential is interpreted by expanding it as a power series. There are no delicate questions of convergence of this series when it operates on polynomials, since all but finitely many terms vanish.
Since the power-series coefficients of the exponential are well known, and higher-order derivatives of the monomial xn can be written down explicitly, this differential-operator representation gives rise to a concrete formula for the coefficients of Hn that can be used to quickly compute these polynomials.
Since the formal expression for the Weierstrass transform W is eD2, we see that the Weierstrass transform of (√2)nHen(x/√2) is xn. Essentially the Weierstrass transform thus turns a series of Hermite polynomials into a corresponding Maclaurin series.
The existence of some formal power series g(D) with nonzero constant coefficient, such that Hen(x) = g(D)xn, is another equivalent to the statement that these polynomials form an Appell sequence. Since they are an Appell sequence, they are a fortiori a Sheffer sequence.
Contour-integral representation
From the generating-function representation above, we see that the Hermite polynomials have a representation in terms of a contour integral, as
with the contour encircling the origin.
Generalizations
The probabilist's Hermite polynomials defined above are orthogonal with respect to the standard normal probability distribution, whose density function is
which has expected value 0 and variance 1.
Scaling, one may analogously speak of generalized Hermite polynomials[9]
of variance α, where α is any positive number. These are then orthogonal with respect to the normal probability distribution whose density function is
They are given by
Now, if
then the polynomial sequence whose nth term is
is called the umbral composition of the two polynomial sequences. It can be shown to satisfy the identities
and
The last identity is expressed by saying that this parameterized family of polynomial sequences is known as a cross-sequence. (See the above section on Appell sequences and on the differential-operator representation, which leads to a ready derivation of it. This binomial type identity, for α = β = 1/2, has already been encountered in the above section on #Recursion relations.)
"Negative variance"
Since polynomial sequences form a group under the operation of umbral composition, one may denote by
the sequence that is inverse to the one similarly denoted, but without the minus sign, and thus speak of Hermite polynomials of negative variance. For α > 0, the coefficients of are just the absolute values of the corresponding coefficients of .
These arise as moments of normal probability distributions: The nth moment of the normal distribution with expected value μ and variance σ2 is
where X is a random variable with the specified normal distribution. A special case of the cross-sequence identity then says that
Applications
Hermite functions
One can define the Hermite functions (often called Hermite-Gaussian functions) from the physicist's polynomials:
Thus,
Since these functions contain the square root of the weight function and have been scaled appropriately, they are orthonormal:
and they form an orthonormal basis of L2(R). This fact is equivalent to the corresponding statement for Hermite polynomials (see above).
The Hermite functions are closely related to the Whittaker function (Whittaker & Watson 1996) Dn(z):
and thereby to other parabolic cylinder functions.
The Hermite functions satisfy the differential equation
This equation is equivalent to the Schrödinger equation for a harmonic oscillator in quantum mechanics, so these functions are the eigenfunctions.
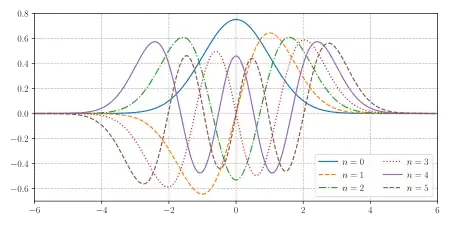
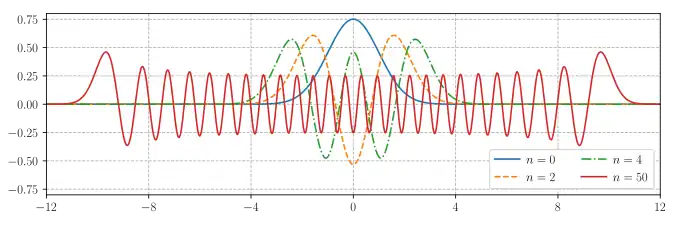
Recursion relation
Following recursion relations of Hermite polynomials, the Hermite functions obey
and
Extending the first relation to the arbitrary mth derivatives for any positive integer m leads to
This formula can be used in connection with the recurrence relations for Hen and ψn to calculate any derivative of the Hermite functions efficiently.
Cramér's inequality
For real x, the Hermite functions satisfy the following bound due to Harald Cramér[10][11] and Jack Indritz:[12]
Hermite functions as eigenfunctions of the Fourier transform
The Hermite functions ψn(x) are a set of eigenfunctions of the continuous Fourier transform F. To see this, take the physicist's version of the generating function and multiply by e−1/2x2. This gives
The Fourier transform of the left side is given by
The Fourier transform of the right side is given by
Equating like powers of t in the transformed versions of the left and right sides finally yields
The Hermite functions ψn(x) are thus an orthonormal basis of L2(R), which diagonalizes the Fourier transform operator.[13]
Wigner distributions of Hermite functions
The Wigner distribution function of the nth-order Hermite function is related to the nth-order Laguerre polynomial. The Laguerre polynomials are
leading to the oscillator Laguerre functions
For all natural integers n, it is straightforward to see[14] that
where the Wigner distribution of a function x ∈ L2(R, C) is defined as
This is a fundamental result for the quantum harmonic oscillator discovered by Hip Groenewold in 1946 in his PhD thesis.[15] It is the standard paradigm of quantum mechanics in phase space.
There are further relations between the two families of polynomials.
Combinatorial interpretation of coefficients
In the Hermite polynomial Hen(x) of variance 1, the absolute value of the coefficient of xk is the number of (unordered) partitions of an n-element set into k singletons and n − k/2 (unordered) pairs. Equivalently, it is the number of involutions of an n-element set with precisely k fixed points, or in other words, the number of matchings in the complete graph on n vertices that leave k vertices uncovered (indeed, the Hermite polynomials are the matching polynomials of these graphs). The sum of the absolute values of the coefficients gives the total number of partitions into singletons and pairs, the so-called telephone numbers
This combinatorial interpretation can be related to complete exponential Bell polynomials as
where xi = 0 for all i > 2.
These numbers may also be expressed as a special value of the Hermite polynomials:[16]
Completeness relation
The Christoffel–Darboux formula for Hermite polynomials reads
Moreover, the following completeness identity for the above Hermite functions holds in the sense of distributions:
where δ is the Dirac delta function, ψn the Hermite functions, and δ(x − y) represents the Lebesgue measure on the line y = x in R2, normalized so that its projection on the horizontal axis is the usual Lebesgue measure.
This distributional identity follows Wiener (1958) by taking u → 1 in Mehler's formula, valid when −1 < u < 1:
which is often stated equivalently as a separable kernel,[17][18]
The function (x, y) → E(x, y; u) is the bivariate Gaussian probability density on R2, which is, when u is close to 1, very concentrated around the line y = x, and very spread out on that line. It follows that
when f and g are continuous and compactly supported.
This yields that f can be expressed in Hermite functions as the sum of a series of vectors in L2(R), namely,
In order to prove the above equality for E(x,y;u), the Fourier transform of Gaussian functions is used repeatedly:
The Hermite polynomial is then represented as
With this representation for Hn(x) and Hn(y), it is evident that
and this yields the desired resolution of the identity result, using again the Fourier transform of Gaussian kernels under the substitution
See also
Notes
- Laplace (1811). "Mémoire sur les intégrales définies et leur application aux probabilités, et spécialement a la recherche du milieu qu'il faut choisir entre les resultats des observations" [Memoire on definite integrals and their application to probabilities, and especially to the search for the mean which must be chosen among the results of observations]. Mémoires de la Classe des Sciences Mathématiques et Physiques de l'Institut Impérial de France (in French). 11: 297–347.
- Laplace, P.-S. (1812), Théorie analytique des probabilités [Analytic Probability Theory], vol. 2, pp. 194–203 Collected in Œuvres complètes VII.
- Tchébychef, P. (1860). "Sur le développement des fonctions à une seule variable" [On the development of single-variable functions]. Bulletin de l'Académie impériale des sciences de St.-Pétersbourg (in French). 1: 193–200. Collected in Œuvres I, 501–508.
- Hermite, C. (1864). "Sur un nouveau développement en série de fonctions" [On a new development in function series]. C. R. Acad. Sci. Paris (in French). 58: 93–100. Collected in Œuvres II, 293–303.
- Tom H. Koornwinder, Roderick S. C. Wong, and Roelof Koekoek et al. (2010) and Abramowitz & Stegun.
- "18. Orthogonal Polynomials, Classical Orthogonal Polynomials, Sums". Digital Library of Mathematical Functions. National Institute of Standards and Technology. Retrieved 30 January 2015.
- Abramowitz & Stegun 1983, p. 508–510, 13.6.38 and 13.5.16.
- Szegő 1955, p. 201
- Roman, Steven (1984), The Umbral Calculus, Pure and Applied Mathematics, vol. 111 (1st ed.), Academic Press, pp. 87–93, ISBN 978-0-12-594380-2
- Erdélyi et al. 1955, p. 207.
- Szegő 1955.
- Indritz, Jack (1961), "An inequality for Hermite polynomials", Proceedings of the American Mathematical Society, 12 (6): 981–983, doi:10.1090/S0002-9939-1961-0132852-2, MR 0132852
- In this case, we used the unitary version of the Fourier transform, so the eigenvalues are (−i)n. The ensuing resolution of the identity then serves to define powers, including fractional ones, of the Fourier transform, to wit a Fractional Fourier transform generalization, in effect a Mehler kernel.
- Folland, G. B. (1989), Harmonic Analysis in Phase Space, Annals of Mathematics Studies, vol. 122, Princeton University Press, ISBN 978-0-691-08528-9
- Groenewold, H. J. (1946). "On the Principles of elementary quantum mechanics". Physica. 12 (7): 405–460. Bibcode:1946Phy....12..405G. doi:10.1016/S0031-8914(46)80059-4.
- Banderier, Cyril; Bousquet-Mélou, Mireille; Denise, Alain; Flajolet, Philippe; Gardy, Danièle; Gouyou-Beauchamps, Dominique (2002), "Generating functions for generating trees", Discrete Mathematics, 246 (1–3): 29–55, arXiv:math/0411250, doi:10.1016/S0012-365X(01)00250-3, MR 1884885, S2CID 14804110
- Mehler, F. G. (1866), "Ueber die Entwicklung einer Function von beliebig vielen Variabeln nach Laplaceschen Functionen höherer Ordnung" [On the development of a function of arbitrarily many variables according to higher-order Laplace functions], Journal für die Reine und Angewandte Mathematik (in German) (66): 161–176, ISSN 0075-4102, ERAM 066.1720cj. See p. 174, eq. (18) and p. 173, eq. (13).
- Erdélyi et al. 1955, p. 194, 10.13 (22).
References
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 22". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 773. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Courant, Richard; Hilbert, David (1989) [1953], Methods of Mathematical Physics, vol. 1, Wiley-Interscience, ISBN 978-0-471-50447-4
- Erdélyi, Arthur; Magnus, Wilhelm; Oberhettinger, Fritz; Tricomi, Francesco G. (1955), Higher transcendental functions (PDF), vol. II, McGraw-Hill, ISBN 978-0-07-019546-2
- Fedoryuk, M.V. (2001) [1994], "Hermite function", Encyclopedia of Mathematics, EMS Press
- Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), "Orthogonal Polynomials", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
- Laplace, P. S. (1810), "Mémoire sur les intégrales définies et leur application aux probabilités, et spécialement a la recherche du milieu qu'il faut choisir entre les résultats des observations", Mémoires de l'Académie des Sciences: 279–347 Oeuvres complètes 12, pp.357-412, English translation Archived 2016-03-04 at the Wayback Machine.
- Shohat, J.A.; Hille, Einar; Walsh, Joseph L. (1940), A bibliography on orthogonal polynomials, Bulletin of the National Research Council, vol. Number 103, Washington D.C.: National Academy of Sciences - 2000 references of Bibliography on Hermite polynomials.
- Suetin, P. K. (2001) [1994], "Hermite polynomials", Encyclopedia of Mathematics, EMS Press
- Szegő, Gábor (1955) [1939], Orthogonal Polynomials, Colloquium Publications, vol. 23 (4th ed.), American Mathematical Society, ISBN 978-0-8218-1023-1
- Temme, Nico (1996), Special Functions: An Introduction to the Classical Functions of Mathematical Physics, New York: Wiley, ISBN 978-0-471-11313-3
- Wiener, Norbert (1958) [1933], The Fourier Integral and Certain of its Applications (revised ed.), New York: Dover Publications, ISBN 0-486-60272-9
- Whittaker, E. T.; Watson, G. N. (1996) [1927], A Course of Modern Analysis (4th ed.), London: Cambridge University Press, ISBN 978-0-521-58807-2
External links
 Media related to Hermite polynomials at Wikimedia Commons
Media related to Hermite polynomials at Wikimedia Commons- Weisstein, Eric W. "Hermite Polynomial". MathWorld.
- GNU Scientific Library — includes C version of Hermite polynomials, functions, their derivatives and zeros (see also GNU Scientific Library)