Hexagonal tortoise problem
The hexagonal tortoise problem (Korean: 지수귀문도; Hanja: 地數龜文圖; RR: jisugwimundo) was invented by Korean aristocrat and mathematician Choi Seok-jeong (1646–1715). It is a mathematical problem that involves a hexagonal lattice, like the hexagonal pattern on some tortoises' shells, to the (N) vertices of which must be assigned integers (from 1 to N) in such a way that the sum of all integers at the vertices of each hexagon is the same.[1] The problem has apparent similarities to a magic square although it is a vertex-magic format rather than an edge-magic form or the more typical rows-of-cells form.[1]
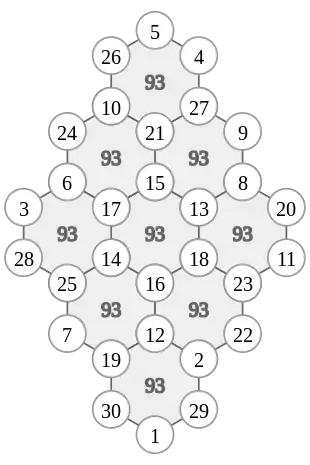
Choi Seok-jeong's original magic hexagonal tortoise pattern. All the sums of six numbers of each hexagon are the same number, 93. The magic sum varies if the numbers 1 through 30 are rearranged. For example, the magic sum could be 77 through 109.
His book, Gusuryak, contains many mathematical discoveries.
References
- Choe, Choi & Moon 2003, p. 850.
Sources used
- Choe, Heemahn; Choi, Sung-Soon; Moon, Byung-Ro (2003). Cantù-Paz, Erick (ed.). A Hybrid Genetic Algorithm for the Hexagonal Tortoise Problem. Proceedings of the Genetic and Evolutionary Computation (GECCO) Conference, Chicago, IL, USA, July 12–16, 2003. Springer. ISBN 978-3-540-40602-0.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.