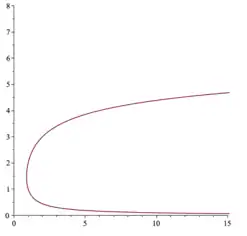
Inverse gamma function

In mathematics, the inverse gamma function $\Gamma ^{-1}(x)$ is the inverse function of the gamma function. In other words, $y=\Gamma ^{-1}(x)$ whenever ${\textstyle \Gamma (y)=x}$ . For example, $\Gamma ^{-1}(24)=5$ .[1] Usually, the inverse gamma function refers to the principal branch with domain on the real interval $\left[\beta ,+\infty \right)$ and image on the real interval $\left[\alpha ,+\infty \right)$ , where $\beta =0.8856031\ldots$ [2] is the minimum value of the gamma function on the positive real axis and $\alpha =\Gamma ^{-1}(\beta )=1.4616321\ldots$ [3] is the location of that minimum.[4]

Graph of an inverse gamma function

Plot of inverse gamma function in the complex plane

Definition

The inverse gamma function may be defined by the following integral representation[5]

\Gamma ^{-1}(x)=a+bx+\int _{-\infty }^{\Gamma (\alpha )}\left({\frac {1}{x-t}}-{\frac {t}{t^{2}-1}}\right)d\mu (t)

where $\mu (t)$ is a Borel measure such that

\int _{-\infty }^{\Gamma \left(\alpha \right)}\left({\frac {1}{t^{2}+1}}\right)d\mu (t)<\infty \,,

and $a$ and $b$ are real numbers with $b\geqq 0$ .

Approximation

To compute the branches of the inverse gamma function one can first compute the Taylor series of $\Gamma (x)$ near $\alpha$ . The series can then be truncated and inverted, which yields successively better approximations to $\Gamma ^{-1}(x)$ . For instance, we have the quadratic approximation:[6]

\Gamma ^{-1}\left(x\right)\approx \alpha +{\sqrt {\frac {2\left(x-\Gamma \left(\alpha \right)\right)}{\Psi \left(1,\ \alpha \right)\Gamma \left(\alpha \right)}}}.

The inverse gamma function also has the following asymptotic formula[7]

\Gamma ^{-1}(x)\sim {\frac {1}{2}}+{\frac {\ln \left({\frac {x}{\sqrt {2\pi }}}\right)}{W_{0}\left(e^{-1}\ln \left({\frac {x}{\sqrt {2\pi }}}\right)\right)}}

where $W_{0}(x)$ is the Lambert W function. The formula is found by inverting the Stirling approximation, and so can also be expanded into an asymptotic series.

Series expansion

To obtain a series expansion of the inverse gamma function one can first compute the series expansion of the reciprocal gamma function ${\frac {1}{\Gamma (x)}}$ near the poles at the negative integers, and then invert the series.

Setting $z={\frac {1}{x}}$ then yields, for the n th branch $\Gamma _{n}^{-1}(z)$ of the inverse gamma function ( $n\geq 0$ )[8]

\Gamma _{n}^{-1}(z)=-n+{\frac {\left(-1\right)^{n}}{n!z}}+{\frac {\psi ^{(0)}\left(n+1\right)}{\left(n!z\right)^{2}}}+{\frac {\left(-1\right)^{n}\left(\pi ^{2}+9\psi ^{(0)}\left(n+1\right)^{2}-3\psi ^{(1)}\left(n+1\right)\right)}{6\left(n!z\right)^{3}}}+O\left({\frac {1}{z^{4}}}\right)

where $\psi ^{(n)}(x)$ is the polygamma function.

References

Borwein, Jonathan M.; Corless, Robert M. (2017). "Gamma and Factorial in the Monthly". The American Mathematical Monthly. 125 (5): 400–424. arXiv:1703.05349. doi:10.1080/00029890.2018.1420983. JSTOR 48663320. S2CID 119324101.
OEIS: A030171
OEIS: A030169
Uchiyama, Mitsuru (April 2012). "The principal inverse of the gamma function". Proceedings of the American Mathematical Society. 140 (4): 1347. doi:10.1090/S0002-9939-2011-11023-2. JSTOR 41505586. S2CID 85549521.
Pedersen, Henrik (9 September 2013). ""Inverses of gamma functions"". Constructive Approximation. 7 (2): 251–267. arXiv:1309.2167. doi:10.1007/s00365-014-9239-1. S2CID 253898042.
Corless, Robert M.; Amenyou, Folitse Komla; Jeffrey, David (2017). "Properties and Computation of the Functional Inverse of Gamma". 2017 19th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC). International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC). p. 65. doi:10.1109/SYNASC.2017.00020. ISBN 978-1-5386-2626-9. S2CID 53287687.
Amenyou, Folitse Komla; Jeffrey, David (2018). "Properties and Computation of the inverse of the Gamma Function" (MS). p. 28.
Couto, Ana Carolina Camargos; Jeffrey, David; Corless, Robert (November 2020). "The Inverse Gamma Function and its Numerical Evaluation". Maple Conference Proceedings. Section 8.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Borwein, Jonathan M.; Corless, Robert M. (2017). "Gamma and Factorial in the Monthly". The American Mathematical Monthly. 125 (5): 400–424. arXiv:1703.05349. doi:10.1080/00029890.2018.1420983. JSTOR 48663320. S2CID 119324101.

[2] OEIS: A030171

[3] OEIS: A030169

[4] Uchiyama, Mitsuru (April 2012). "The principal inverse of the gamma function". Proceedings of the American Mathematical Society. 140 (4): 1347. doi:10.1090/S0002-9939-2011-11023-2. JSTOR 41505586. S2CID 85549521.

[5] Pedersen, Henrik (9 September 2013). ""Inverses of gamma functions"". Constructive Approximation. 7 (2): 251–267. arXiv:1309.2167. doi:10.1007/s00365-014-9239-1. S2CID 253898042.

[6] Corless, Robert M.; Amenyou, Folitse Komla; Jeffrey, David (2017). "Properties and Computation of the Functional Inverse of Gamma". 2017 19th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC). International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC). p. 65. doi:10.1109/SYNASC.2017.00020. ISBN 978-1-5386-2626-9. S2CID 53287687.

[7] Amenyou, Folitse Komla; Jeffrey, David (2018). "Properties and Computation of the inverse of the Gamma Function" (MS). p. 28.

[8] Couto, Ana Carolina Camargos; Jeffrey, David; Corless, Robert (November 2020). "The Inverse Gamma Function and its Numerical Evaluation". Maple Conference Proceedings. Section 8.