Ion speciation

Speciation of ions refers to the changing concentration of varying forms of an ion as the pH of the solution changes.[1]

The ratio of acid, AH and conjugate base, A⁻, concentrations varies as the difference between the pH and the pK_a varies, in accordance with the Henderson-Hasselbalch equation.

The pH of a solution of a monoprotic weak acid can be expressed in terms of the extent of dissociation. After rearranging the expression defining the acid dissociation constant, and putting pH = −log₁₀[H⁺], one obtains

pH = pK_a – log ( [AH]/[A⁻] )

This is a form of the Henderson-Hasselbalch equation. It can be deduced from this expression that

• when the acid is 1 % dissociated, that is, when [AH]/[A⁻] = 100, pH = pK_a − 2
• when the acid is 50 % dissociated, that is, when [AH]/[A⁻] = 1, pH = pK_a
• when the acid is 99 % dissociated, that is, when [AH]/[A⁻] = 0.01, pH = pK_a + 2

It follows that the range of pH within which there is partial dissociation of the acid is about pK_a ± 2. This is shown graphically at the right.

A practical application of these results is that the pH transition range of a pH indicator is approximately pK_a ± 1; the colour of the indicator in its acid form is different from the colour of the conjugate base form. In the transition range both forms are in equilibrium, so the colour is intermediate. Outside the transition range the concentration of acid or conjugate base is less than 10 % and the colour of the major species dominates.

Species concentrations calculated with the program HySS for a 10 mM solution of citric acid. pK_a1 = 3.13, pK_a2 = 4.76, pK_a3 = 6.40.

A weak acid may be defined as an acid with pK_a greater than about −2. An acid with pK_a = −2 would be 99 % dissociated at pH 0, that is, in a 1 M HCl solution. Any acid with a pK_a less than about −2 is said to be a strong acid. Strong acids are said to be fully dissociated. There is no precise pK_a value that distinguishes between strong and weak acids because strong acids, such as sulfuric acid, are associated in very concentrated solution.

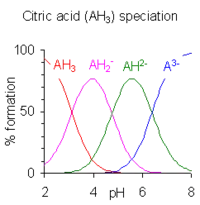
Calculation of the species concentrations for a polyprotic acid is more complicated unless the pK values are separated by four or more, because three or more species may co-exist at a given pH. The example of citric acid is shown at the right. The pH regions in which the species exist overlap extensively since the difference between successive pK_a values is small. A large number of computer programs for the calculation of equilibrium species concentrations have been published. Most of them can handle much more complicated equilibria than acid-base equilibria in solution. For details concerning general purpose programs see computer programs for calculating species concentrations in chemical equilibrium.