Isbell's zigzag theorem

The blue dashed line is the spine of the zig-zag.

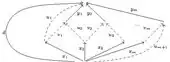
Zig-zag:[6][2][7][8][9][note 1] If U is a submonoid of a monoid (or a subsemigroup of a semigroup) S, then a system of equalities;

${\displaystyle {\begin{aligned}d&=x_{1}u_{1},&u_{1}&=v_{1}y_{1}\\x_{i-1}v_{i-1}&=x_{i}u_{i},&u_{i}y_{i-1}&=v_{i}y_{i}\;(i=2,\dots ,m)\\x_{m}v_{m}&=u_{m+1},&u_{m+1}y_{m}&=d\end{aligned}}}$

in which ${\displaystyle u_{1},\dots ,u_{m+1},v_{1},\dots ,v_{m}\in U}$ and ${\displaystyle x_{1},\dots ,x_{m},y_{1},\dots ,y_{m}\in S}$, is called a zig-zag of length m in S over U with value d. By the spine of the zig-zag we mean the ordered (2m + 1)-tuple ${\displaystyle (u_{1},v_{1},u_{2},v_{2},\dots ,u_{m},v_{m},u_{m+1})}$.

Dominion:[5][11] Let U is a submonoid of a monoid (or a subsemigroup of a semigroup) S. The dominion ${\displaystyle {\rm {{Dom}_{S}(U)}}}$ is the set of all elements ${\displaystyle s\in S}$ such that, for all homomorphisms ${\displaystyle f,g:S\to T}$ coinciding on U, ${\displaystyle f(s)=g(s)}$.

We call a subsemigroup U of a semigroup U closed if ${\displaystyle {\rm {{Dom}_{S}(U)=U}}}$, and dense if ${\displaystyle {\rm {{Dom}_{S}(U)=S}}}$.[2][12]

Isbell's zigzag theorem:[13]

If U is a submonoid of a monoid S then ${\displaystyle d\in {\rm {{Dom}_{S}(U)}}}$ if and only if either ${\displaystyle d\in U}$ or there exists a zig-zag in S over U with value d that is, there is a sequence of factorizations of d of the form

${\displaystyle d=x_{1}u_{1}=x_{1}v_{1}y_{1}=x_{2}u_{2}y_{1}=x_{2}v_{2}y_{2}=\cdots =x_{m}v_{m}y_{m}=u_{m+1}y_{m}}$

This statement also holds for semigroups.[6][14][8][4][9]

For monoids, this theorem can be written more concisely:[15][2][16]

Let S be a monoid, let U be a submonoid of S, and let ${\displaystyle d\in S}$. Then ${\displaystyle d\in \mathrm {Dom} _{S}(U)}$ if and only if ${\displaystyle d\otimes 1=1\otimes d}$ in the tensor product ${\displaystyle S\otimes _{U}S}$.