Isocline
Given a family of curves, assumed to be differentiable, an isocline for that family is formed by the set of points at which some member of the family attains a given slope. The word comes from the Greek words ἴσος (isos), meaning "same", and the κλίνειν, meaning "make to slope". Generally, an isocline will itself have the shape of a curve or the union of a small number of curves.
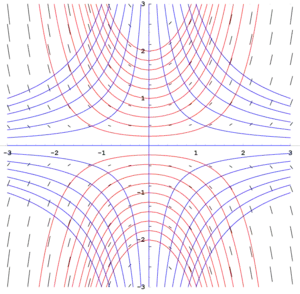
Isoclines are often used as a graphical method of solving ordinary differential equations. In an equation of the form y' = f(x, y), the isoclines are lines in the (x, y) plane obtained by setting f(x, y) equal to a constant. This gives a series of lines (for different constants) along which the solution curves have the same gradient. By calculating this gradient for each isocline, the slope field can be visualised; making it relatively easy to sketch approximate solution curves; as in fig. 1.
Other uses
In population dynamics, the term "zero-growth isocline" refers to the set of population sizes at which the rate of change for one population in a pair of interacting populations is zero.[1] However, this is rare and a more common term is nullcline.
References
- "INTERSPECIFIC COMPETITION: LOTKA-VOLTERRA". Archived from the original on 17 May 2021. Retrieved 6 March 2019.
- Hanski, I. (1999) Metapopulation Ecology. Oxford University Press, Oxford, pp. 43–46.
- Mathworld: Isocline