Jaynes–Cummings–Hubbard model

The Hamiltonian of the JCH model is (${\displaystyle \hbar =1}$):

${\displaystyle H=\sum _{n=1}^{N}\omega _{c}a_{n}^{\dagger }a_{n}+\sum _{n=1}^{N}\omega _{a}\sigma _{n}^{+}\sigma _{n}^{-}+\kappa \sum _{n=1}^{N}\left(a_{n+1}^{\dagger }a_{n}+a_{n}^{\dagger }a_{n+1}\right)+\eta \sum _{n=1}^{N}\left(a_{n}\sigma _{n}^{+}+a_{n}^{\dagger }\sigma _{n}^{-}\right)}$

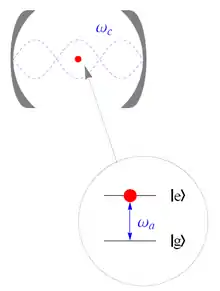
where ${\displaystyle \sigma _{n}^{\pm }}$ are Pauli operators for the two-level atom at the n-th cavity. The ${\displaystyle \kappa }$ is the tunneling rate between neighboring cavities, and ${\displaystyle \eta }$ is the vacuum Rabi frequency which characterizes to the photon-atom interaction strength. The cavity frequency is ${\displaystyle \omega _{c}}$ and atomic transition frequency is ${\displaystyle \omega _{a}}$. The cavities are treated as periodic, so that the cavity labelled by n = N+1 corresponds to the cavity n = 1.[3] Note that the model exhibits quantum tunneling; this process is similar to the Josephson effect.[6][7]

Defining the photonic and atomic excitation number operators as ${\displaystyle {\hat {N}}_{c}\equiv \sum _{n=1}^{N}a_{n}^{\dagger }a_{n}}$ and ${\displaystyle {\hat {N}}_{a}\equiv \sum _{n=1}^{N}\sigma _{n}^{+}\sigma _{n}^{-}}$, the total number of excitations is a conserved quantity, i.e., ${\displaystyle \lbrack H,{\hat {N}}_{c}+{\hat {N}}_{a}\rbrack =0}$.

The JCH Hamiltonian supports two-polariton bound states when the photon-atom interaction is sufficiently strong. In particular, the two polaritons associated with the bound states exhibit a strong correlation such that they stay close to each other in position space.[8] This process is similar to the formation of a bound pair of repulsive bosonic atoms in an optical lattice.[9][10][11]