K-D heap
A K-D heap[1] is a data structure in computer science which implements a multidimensional priority queue without requiring additional space. It is a generalization of the Heap.[2] It allows for efficient insertion, query of the minimum element, and deletion of the minimum element in any of the k dimensions, and therefore includes the double-ended heap as a special case.
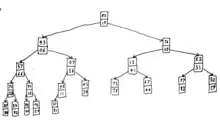
Structure
Given a collection of n items, where each has keys (or priorities), the K-D heap organizes them in to a binary tree which satisfies two conditions:
- It is a complete binary tree, which means it is full except for possibly the last layer, where it must be filled-up from the left.
- It satisfies k-d heap order.
The property of k-d heap order is analogous to that of the heap property for regular heaps. A heap maintains k-d heap order if:
- The node at the root has the smallest 1st-property of the whole tree, and
- Every other node v that is not the root, is such that if its parent w has the smallest i-th property of the subtree rooted by the parent, then v has the smallest -th property of the whole subtree rooted by v.
One consequence of this structure is that the smallest 1-st property-element will trivially be in the root, and moreover all the smallest i-th property elements for every i will be in the first k levels.
Operations
Creating a K-D heap from n items takes O(n) time. The following operations are supported:
- Insert a new item in time O(log n)
- Retrieve the item with a minimum key in any of the dimensions in constant time
- Delete an item with a minimum key in any dimension in time O(log n)
- Delete or modify an arbitrary item in the heap in time O(log n) assuming its position in the heap is known
Importantly, the hidden constant in these operations is exponentially large relative , the number of dimensions, so K-D heaps are not practical for applications with very many dimensions.
References
- Ding Y., Weiss M.A. (1993) The K-D heap: An efficient multi-dimensional priority queue. In: Dehne F., Sack JR., Santoro N., Whitesides S. (eds) Algorithms and Data Structures. WADS 1993. Lecture Notes in Computer Science, vol 709. Springer, Berlin, Heidelberg
- Advanced Data Structures, Peter Brass, ISBN 978-0-521-88037-4, page 270