k-mer
In bioinformatics, k-mers are substrings of length contained within a biological sequence. Primarily used within the context of computational genomics and sequence analysis, in which k-mers are composed of nucleotides (i.e. A, T, G, and C), k-mers are capitalized upon to assemble DNA sequences,[1] improve heterologous gene expression,[2][3] identify species in metagenomic samples,[4] and create attenuated vaccines.[5] Usually, the term k-mer refers to all of a sequence's subsequences of length , such that the sequence AGAT would have four monomers (A, G, A, and T), three 2-mers (AG, GA, AT), two 3-mers (AGA and GAT) and one 4-mer (AGAT). More generally, a sequence of length will have k-mers and total possible k-mers, where is number of possible monomers (e.g. four in the case of DNA).
Introduction
k-mers are simply length subsequences. For example, all the possible k-mers of a DNA sequence are shown below:
| k | k-mers |
|---|---|
| 1 | G, T, A, C |
| 2 | GT, TA, AG, GA, AG, GC, CT, TG |
| 3 | GTA, TAG, AGA, GAG, AGC, GCT, CTG, TGT |
| 4 | GTAG, TAGA, AGAG, GAGC, AGCT, GCTG, CTGT |
| 5 | GTAGA, TAGAG, AGAGC, GAGCT, AGCTG, GCTGT |
| 6 | GTAGAG, TAGAGC, AGAGCT, GAGCTG, AGCTGT |
| 7 | GTAGAGC, TAGAGCT, AGAGCTG, GAGCTGT |
| 8 | GTAGAGCT, TAGAGCTG, AGAGCTGT |
| 9 | GTAGAGCTG, TAGAGCTGT |
| 10 | GTAGAGCTGT |
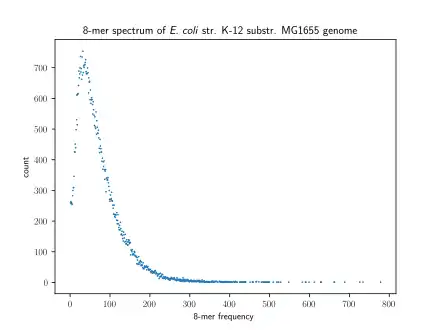
A method of visualizing k-mers, the k-mer spectrum, shows the multiplicity of each k-mer in a sequence versus the number of k-mers with that multiplicity.[6] The number of modes in a k-mer spectrum for a species's genome varies, with most species having a unimodal distribution.[7] However, all mammals have a multimodal distribution. The number of modes within a k-mer spectrum can vary between regions of genomes as well: humans have unimodal k-mer spectra in 5' UTRs and exons but multimodal spectra in 3' UTRs and introns.
Forces Affecting DNA k-mer Frequency
The frequency of k-mer usage is affected by numerous forces, working at multiple levels, which are often in conflict. It is important to note that k-mers for higher values of k are affected by the forces affecting lower values of k as well. For example, if the 1-mer A does not occur in a sequence, none of the 2-mers containing A (AA, AT, AG, and AC) will occur either, thereby linking the effects of the different forces.
k = 1
When k = 1, there are four DNA k-mers, i.e., A, T, G, and C. At the molecular level, there are three hydrogen bonds between G and C, whereas there are only two between A and T. GC bonds, as a result of the extra hydrogen bond (and stronger stacking interactions), are more thermally stable than AT bonds.[8] Mammals and birds have a higher ratio of Gs and Cs to As and Ts (GC-content), which led to the hypothesis that thermal stability was a driving factor of GC-content variation.[9] However, while promising, this hypothesis did not hold up under scrutiny: analysis among a variety of prokaryotes showed no evidence of GC-content correlating with temperature as the thermal adaptation hypothesis would predict.[10] Indeed, if natural selection were to be the driving force behind GC-content variation, that would require that single nucleotide changes, which are often silent, to alter the fitness of an organism.[11]
Rather, current evidence suggests that GC‐biased gene conversion (gBGC) is a driving factor behind variation in GC content.[11] gBGC is a process that occurs during recombination which replaces As and Ts with Gs and Cs.[12] This process, though distinct from natural selection, can nevertheless exert selective pressure on DNA biased towards GC replacements being fixed in the genome. gBGC can therefore be seen as an "impostor" of natural selection. As would be expected, GC content is greater at sites experiencing greater recombination.[13] Furthermore, organisms with higher rates of recombination exhibit higher GC content, in keeping with the gBGC hypothesis's predicted effects.[14] Interestingly, gBGC does not appear to be limited to eukaryotes.[15] Asexual organisms such as bacteria and archaea also experience recombination by means of gene conversion, a process of homologous sequence replacement resulting in multiple identical sequences throughout the genome.[16] That recombination is able to drive up GC content in all domains of life suggests that gBGC is universally conserved. Whether gBGC is a (mostly) neutral byproduct of the molecular machinery of life or is itself under selection remains to be determined. The exact mechanism and evolutionary advantage or disadvantage of gBGC is currently unknown.[17]
k = 2
Despite the comparatively large body of literature discussing GC-content biases, relatively little has been written about dinucleotide biases. What is known is that these dinucleotide biases are relatively constant throughout the genome, unlike GC-content, which, as seen above, can vary considerably.[18] This is an important insight that must not be overlooked. If dinucleotide bias were subject to pressures resulting from translation, then there would be differing patterns of dinucleotide bias in coding and noncoding regions driven by some dinucelotides' reduced translational efficiency.[19] Because there is not, it can therefore be inferred that the forces modulating dinucleotide bias are independent of translation. Further evidence against translational pressures affecting dinucleotide bias is the fact that the dinucleotide biases of viruses, which rely heavily on translational efficiency, are shaped by their viral family more than by their hosts, whose translational machinery the viruses hijack.[20]
Counter to gBGC's increasing GC-content is CG suppression, which reduces the frequency of CG 2-mers due to deamination of methylated CG dinucleotides, resulting in substitutions of CGs with TGs, thereby reducing the GC-content.[21] This interaction highlights the interrelationship between the forces affecting k-mers for varying values of k.
One interesting fact about dinucleotide bias is that it can serve as a "distance" measurement between phylogenetically similar genomes. The genomes of pairs of organisms that are closely related share more similar dinucleotide biases than between pairs of more distantly related organisms.[18]
k = 3
There are twenty natural amino acids that are used to build the proteins that DNA encodes. However, there are only four nucleotides. Therefore, there cannot be a one-to-one correspondence between nucleotides and amino acids. Similarly, there are 16 2-mers, which is also not enough to unambiguously represent every amino acid. However, there are 64 distinct 3-mers in DNA, which is enough to uniquely represent each amino acid. These non-overlapping 3-mers are called codons. While each codon only maps to one amino acid, each amino acid can be represented by multiple codons. Thus, the same amino acid sequence can have multiple DNA representations. Interestingly, each codon for an amino acid is not used in equal proportions.[22] This is called codon-usage bias (CUB). When k = 3, a distinction must be made between true 3-mer frequency and CUB. For example, the sequence ATGGCA has four 3-mer words within it (ATG, TGG, GGC, and GCA) while only containing two codons (ATG and GCA). However, CUB is a major driving factor of 3-mer usage bias (accounting for up to ⅓ of it, since ⅓ of the k-mers in a coding region are codons) and will be the main focus of this section.
The exact cause of variation between the frequencies of various codons is not fully understood. It is known that codon preference is correlated with tRNA abundances, with codons matching more abundant tRNAs being correspondingly more frequent[22] and that more highly expressed proteins exhibit greater CUB.[23] This suggests that selection for translational efficiency or accuracy is the driving force behind CUB variation.
k = 4
Similar to the effect seen in dinucleotide bias, the tetranucleotide biases of phylogenetically similar organisms are more similar than between less closely related organisms.[4] The exact cause of variation in tetranucleotide bias is not well understood, but it has been hypothesized to be the result of the maintenance of genetic stability at the molecular level.[24]
Applications
The frequency of a set of k-mers in a species's genome, in a genomic region, or in a class of sequences can be used as a "signature" of the underlying sequence. Comparing these frequencies is computationally easier than sequence alignment and is an important method in alignment-free sequence analysis. It can also be used as a first stage analysis before an alignment.
Sequence assembly
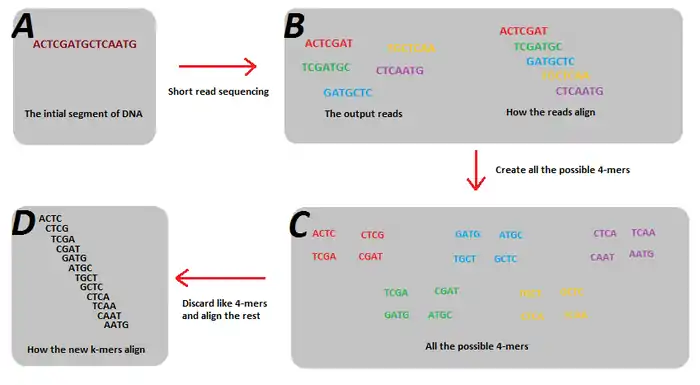
In sequence assembly, k-mers are used during the construction of De Bruijn graphs.[25][26] In order to create a De Bruijn Graph, the k-mers stored in each edge with length must overlap another string in another edge by in order to create a vertex. Reads generated from next-generation sequencing will typically have different read lengths being generated. For example, reads by Illumina’s sequencing technology capture reads of 100-mers. However, the problem with the sequencing is that only small fractions out of all the possible 100-mers that are present in the genome are actually generated. This is due to read errors, but more importantly, just simple coverage holes that occur during sequencing. The problem is that these small fractions of the possible k-mers violate the key assumption of De Bruijn graphs that all the k-mer reads must overlap its adjoining k-mer in the genome by (which cannot occur when all the possible k-mers are not present).
The solution to this problem is to break these k-mer sized reads into smaller k-mers, such that the resulting smaller k-mers will represent all the possible k-mers of that smaller size that are present in the genome.[27] Furthermore, splitting the k-mers into smaller sizes also helps alleviate the problem of different initial read lengths. In this example, the five reads do not account for all the possible 7-mers of the genome, and as such, a De Bruijn graph cannot be created. But, when they are split into 4-mers, the resultant subsequences are enough to reconstruct the genome using a De Bruijn graph.
Beyond being used directly for sequence assembly, k-mers can also be used to detect genome mis-assembly by identifying k-mers that are overrepresented which suggest the presence of repeated DNA sequences that have been combined.[28] In addition, k-mers are also used to detect bacterial contamination during eukaryotic genome assembly, an approach borrowed from the field of metagenomics.[29][30]
Choice of k-mer size
The choice of the k-mer size has many different effects on the sequence assembly. These effects vary greatly between lower sized and larger sized k-mers. Therefore, an understanding of the different k-mer sizes must be achieved in order to choose a suitable size that balances the effects. The effects of the sizes are outlined below.
Lower k-mer sizes
- A lower k-mer size will decrease the amount of edges stored in the graph, and as such, will help decrease the amount of space required to store DNA sequence.
- Having smaller sizes will increase the chance for all the k-mers to overlap, and as such, have the required subsequences in order to construct the De Bruijn graph.[31]
- However, by having smaller sized k-mers, you also risk having many vertices in the graph leading into a single k-mer. Therefore, this will make the reconstruction of the genome more difficult as there is a higher level of path ambiguities due to the larger amount of vertices that will need to be traversed.
- Information is lost as the k-mers become smaller.
- E.g. The possibility of AGTCGTAGATGCTG is lower than ACGT, and as such, holds a greater amount of information (refer to entropy (information theory) for more information).
- Smaller k-mers also have the problem of not being able to resolve areas in the DNA where small microsatellites or repeats occur. This is because smaller k-mers will tend to sit entirely within the repeat region and is therefore hard to determine the amount of repetition that has actually taken place.
- E.g. For the subsequence ATGTGTGTGTGTGTACG, the amount of repetitions of TG will be lost if a k-mer size less than 16 is chosen. This is because most of the k-mers will sit in the repeated region and may just be discarded as repeats of the same k-mer instead of referring the amount of repeats.
Higher k-mer sizes
- Having larger sized k-mers will increase the number of edges in the graph, which in turn, will increase the amount of memory needed to store the DNA sequence.
- By increasing the size of the k-mers, the number of vertices will also decrease. This will help with the construction of the genome as there will be fewer paths to traverse in the graph.[31]
- Larger k-mers also run a higher risk of not having outward vertices from every k-mer. This is due to larger k-mers increasing the risk that it will not overlap with another k-mer by . Therefore, this can lead to disjoints in the reads, and as such, can lead to a higher amount of smaller contigs.
- Larger k-mer sizes help alleviate the problem of small repeat regions. This is due to the fact that the k-mer will contain a balance of the repeat region and the adjoining DNA sequences (given it are a large enough size) that can help to resolve the amount of repetition in that particular area.
Genetics and Genomics
With respect to disease, dinucleotide bias has been applied to the detection of genetic islands associated with pathogenicity.[11] Prior work has also shown that tetranucleotide biases are able to effectively detect horizontal gene transfer in both prokaryotes[32] and eukaryotes.[33]
Another application of k-mers is in genomics-based taxonomy. For example, GC-content has been used to distinguish between species of Erwinia with moderate success.[34] Similar to the direct use of GC-content for taxonomic purposes is the use of Tm, the melting temperature of DNA. Because GC bonds are more thermally stable, sequences with higher GC content exhibit a higher Tm. In 1987, the Ad Hoc Committee on Reconciliation of Approaches to Bacterial Systematics proposed the use of ΔTm as factor in determining species boundaries as part of the phylogenetic species concept, though this proposal does not appear to have gained traction within the scientific community.[35]
Other applications within genetics and genomics include:
- RNA isoform quantification from RNA-seq data[36]
- Classification of human mitochondrial haplogroup[37]
- Detection of recombination sites in genomes[38]
- Estimation of genome size using k-mer frequency vs k-mer depth[39][40]
- Characterization of CpG islands by flanking regions[41][42]
- De novo detection of repeated sequence such as transposable element[43]
- DNA barcoding of species.[7][44]
- Characterization of protein-binding sequence motifs[45]
- Identification of mutation or polymorphism using next generation sequencing data[46]
Metagenomics
k-mer frequency and spectrum variation is heavily used in metagenomics for both analysis[47][48] and binning. In binning, the challenge is to separate sequencing reads into "bins" of reads for each organism (or operational taxonomic unit), which will then be assembled. TETRA is a notable tool that takes metagenomic samples and bins them into organisms based on their tetranucleotide (k = 4) frequencies.[49] Other tools that similarly rely on k-mer frequency for metagenomic binning are CompostBin (k = 6),[50] PCAHIER,[51] PhyloPythia (5 ≤ k ≤ 6),[52] CLARK (k ≥ 20),[53] and TACOA (2 ≤ k ≤ 6).[54] Recent developments have also applied deep learning to metagenomic binning using k-mers.[55]
Other applications within metagenomics include:
- Recovery of reading frames from raw reads[56]
- Estimation of species abundance in metagenomic samples[57]
- Determination of which species are present in samples[58][59]
- Identification of biomarkers for diseases from samples[60]
Biotechnology
Modifying k-mer frequencies in DNA sequences has been used extensively in biotechnological applications to control translational efficiency. Specifically, it has been used to both up- and down-regulate protein production rates.
With respect to increasing protein production, reducing unfavorable dinucleotide frequency has been used yield higher rates of protein synthesis.[61] In addition, codon usage bias has been modified to create synonymous sequences with greater protein expression rates.[2][3] Similarly, codon pair optimization, a combination of dinucelotide and codon optimization, has also been successfully used to increase expression.[62]
The most studied application of k-mers for decreasing translational efficiency is codon-pair manipulation for attenuating viruses in order to create vaccines. Researchers were able to recode dengue virus, the virus that causes dengue fever, such that its codon-pair bias was more different to mammalian codon-usage preference than the wild type.[63] Though containing an identical amino-acid sequence, the recoded virus demonstrated significantly weakened pathogenicity while eliciting a strong immune response. This approach has also been used effectively to create an influenza vaccine[64] as well a vaccine for Marek's disease herpesvirus (MDV).[65] Notably, the codon-pair bias manipulation employed to attenuate MDV did not effectively reduce the oncogenicity of the virus, highlighting a potential weakness in the biotechnology applications of this approach. To date, no codon-pair deoptimized vaccine has been approved for use.
Two later articles help explain the actual mechanism underlying codon-pair deoptimization: codon-pair bias is the result of dinucleotide bias.[66][67] By studying viruses and their hosts, both sets of authors were able to conclude that the molecular mechanism that results in the attenuation of viruses is an increase in dinucleotides poorly suited for translation.
GC-content, due to its effect on DNA melting point, is used to predict annealing temperature in PCR, another important biotechnology tool.
Implementation
Pseudocode
Determining the possible k-mers of a read can be done by simply cycling over the string length by one and taking out each substring of length . The pseudocode to achieve this is as follows:
procedure k-mers(string seq, integer k) is
L ← length(seq)
arr ← new array of L − k + 1 empty strings
// iterate over the number of k-mers in seq,
// storing the nth k-mer in the output array
for n ← 0 to L − k + 1 exclusive do
arr[n] ← subsequence of seq from letter n inclusive to letter n + k exclusive
return arr
In Bioinformatics Pipelines
Because the number of k-mers grows exponentially for values of k, counting k-mers for large values of k (usually >10) is a computationally difficult task. While simple implementations such as the above pseudocode work for small values of k, they need to be adapted for high-throughput applications or when k is large. To solve this problem, various tools have been developed:
- Jellyfish uses a multithreaded, lock-free hash table for k-mer counting and has Python, Ruby, and Perl bindings[68]
- KMC is a tool for k-mer counting that uses a multidisk architecture for optimized speed[69]
- Gerbil uses a hash table approach but with added support for GPU acceleration[70]
- K-mer Analysis Toolkit (KAT) uses a modified version of Jellyfish to analyze k-mer counts[6]
See also
References
 Some of the content in this article was copied from K-mer at the PLOS wiki, which is available under a Creative Commons Attribution 2.5 Generic (CC BY 2.5) license.
Some of the content in this article was copied from K-mer at the PLOS wiki, which is available under a Creative Commons Attribution 2.5 Generic (CC BY 2.5) license.
- Compeau, Phillip E C; Pevzner, Pavel A; Tesler, Glenn (November 2011). "How to apply de Bruijn graphs to genome assembly". Nature Biotechnology. 29 (11): 987–991. doi:10.1038/nbt.2023. ISSN 1087-0156. PMC 5531759. PMID 22068540.
- Welch, Mark; Govindarajan, Sridhar; Ness, Jon E.; Villalobos, Alan; Gurney, Austin; Minshull, Jeremy; Gustafsson, Claes (2009-09-14). Kudla, Grzegorz (ed.). "Design Parameters to Control Synthetic Gene Expression in Escherichia coli". PLOS ONE. 4 (9): e7002. Bibcode:2009PLoSO...4.7002W. doi:10.1371/journal.pone.0007002. ISSN 1932-6203. PMC 2736378. PMID 19759823.
- Gustafsson, Claes; Govindarajan, Sridhar; Minshull, Jeremy (July 2004). "Codon bias and heterologous protein expression". Trends in Biotechnology. 22 (7): 346–353. doi:10.1016/j.tibtech.2004.04.006. PMID 15245907.
- Perry, Scott C.; Beiko, Robert G. (2010-01-01). "Distinguishing Microbial Genome Fragments Based on Their Composition: Evolutionary and Comparative Genomic Perspectives". Genome Biology and Evolution. 2: 117–131. doi:10.1093/gbe/evq004. ISSN 1759-6653. PMC 2839357. PMID 20333228.
- Eschke, Kathrin; Trimpert, Jakob; Osterrieder, Nikolaus; Kunec, Dusan (2018-01-29). Mocarski, Edward (ed.). "Attenuation of a very virulent Marek's disease herpesvirus (MDV) by codon pair bias deoptimization". PLOS Pathogens. 14 (1): e1006857. doi:10.1371/journal.ppat.1006857. ISSN 1553-7374. PMC 5805365. PMID 29377958.
- Mapleson, Daniel; Garcia Accinelli, Gonzalo; Kettleborough, George; Wright, Jonathan; Clavijo, Bernardo J. (2016-10-22). "KAT: a K-mer analysis toolkit to quality control NGS datasets and genome assemblies". Bioinformatics. 33 (4): 574–576. doi:10.1093/bioinformatics/btw663. ISSN 1367-4803. PMC 5408915. PMID 27797770.
- Chor, Benny; Horn, David; Goldman, Nick; Levy, Yaron; Massingham, Tim (2009). "Genomic DNA k-mer spectra: models and modalities". Genome Biology. 10 (10): R108. doi:10.1186/gb-2009-10-10-r108. ISSN 1465-6906. PMC 2784323. PMID 19814784.
- Yakovchuk, P. (2006-01-30). "Base-stacking and base-pairing contributions into thermal stability of the DNA double helix". Nucleic Acids Research. 34 (2): 564–574. doi:10.1093/nar/gkj454. ISSN 0305-1048. PMC 1360284. PMID 16449200.
- Bernardi, Giorgio (January 2000). "Isochores and the evolutionary genomics of vertebrates". Gene. 241 (1): 3–17. doi:10.1016/S0378-1119(99)00485-0. PMID 10607893.
- Hurst, Laurence D.; Merchant, Alexa R. (2001-03-07). "High guanine–cytosine content is not an adaptation to high temperature: a comparative analysis amongst prokaryotes". Proceedings of the Royal Society B: Biological Sciences. 268 (1466): 493–497. doi:10.1098/rspb.2000.1397. ISSN 1471-2954. PMC 1088632. PMID 11296861.
- Mugal, Carina F.; Weber, Claudia C.; Ellegren, Hans (December 2015). "GC-biased gene conversion links the recombination landscape and demography to genomic base composition: GC-biased gene conversion drives genomic base composition across a wide range of species". BioEssays. 37 (12): 1317–1326. doi:10.1002/bies.201500058. PMID 26445215. S2CID 21843897.
- Romiguier, Jonathan; Roux, Camille (2017-02-15). "Analytical Biases Associated with GC-Content in Molecular Evolution". Frontiers in Genetics. 8: 16. doi:10.3389/fgene.2017.00016. ISSN 1664-8021. PMC 5309256. PMID 28261263.
- Spencer, C.C.A. (2006-08-01). "Human polymorphism around recombination hotspots: Figure 1". Biochemical Society Transactions. 34 (4): 535–536. doi:10.1042/BST0340535. ISSN 0300-5127. PMID 16856853.
- Weber, Claudia C; Boussau, Bastien; Romiguier, Jonathan; Jarvis, Erich D; Ellegren, Hans (December 2014). "Evidence for GC-biased gene conversion as a driver of between-lineage differences in avian base composition". Genome Biology. 15 (12): 549. doi:10.1186/s13059-014-0549-1. ISSN 1474-760X. PMC 4290106. PMID 25496599.
- Lassalle, Florent; Périan, Séverine; Bataillon, Thomas; Nesme, Xavier; Duret, Laurent; Daubin, Vincent (2015-02-06). Petrov, Dmitri A. (ed.). "GC-Content Evolution in Bacterial Genomes: The Biased Gene Conversion Hypothesis Expands". PLOS Genetics. 11 (2): e1004941. doi:10.1371/journal.pgen.1004941. ISSN 1553-7404. PMC 4450053. PMID 25659072.
- Santoyo, G; Romero, D (April 2005). "Gene conversion and concerted evolution in bacterial genomes". FEMS Microbiology Reviews. 29 (2): 169–183. doi:10.1016/j.femsre.2004.10.004. PMID 15808740.
- Bhérer, Claude; Auton, Adam (2014-06-16), John Wiley & Sons Ltd (ed.), "Biased Gene Conversion and Its Impact on Genome Evolution", eLS, John Wiley & Sons, Ltd, doi:10.1002/9780470015902.a0020834.pub2, ISBN 9780470015902
- Karlin, Samuel (October 1998). "Global dinucleotide signatures and analysis of genomic heterogeneity". Current Opinion in Microbiology. 1 (5): 598–610. doi:10.1016/S1369-5274(98)80095-7. PMID 10066522.
- Beutler, E.; Gelbart, T.; Han, J. H.; Koziol, J. A.; Beutler, B. (1989-01-01). "Evolution of the genome and the genetic code: selection at the dinucleotide level by methylation and polyribonucleotide cleavage". Proceedings of the National Academy of Sciences. 86 (1): 192–196. Bibcode:1989PNAS...86..192B. doi:10.1073/pnas.86.1.192. ISSN 0027-8424. PMC 286430. PMID 2463621.
- Di Giallonardo, Francesca; Schlub, Timothy E.; Shi, Mang; Holmes, Edward C. (2017-04-15). Dermody, Terence S. (ed.). "Dinucleotide Composition in Animal RNA Viruses Is Shaped More by Virus Family than by Host Species". Journal of Virology. 91 (8). doi:10.1128/JVI.02381-16. ISSN 0022-538X. PMC 5375695. PMID 28148785.
- Żemojtel, Tomasz; kiełbasa, Szymon M.; Arndt, Peter F.; Behrens, Sarah; Bourque, Guillaume; Vingron, Martin (2011-01-01). "CpG Deamination Creates Transcription Factor–Binding Sites with High Efficiency". Genome Biology and Evolution. 3: 1304–1311. doi:10.1093/gbe/evr107. ISSN 1759-6653. PMC 3228489. PMID 22016335.
- Hershberg, R; Petrov, DA (2008). "Selection on Codon Bias". Annual Review of Genetics. 42: 287–299. doi:10.1146/annurev.genet.42.110807.091442. PMID 18983258.
- Sharp, Paul M.; Li, Wen-Hsiung (1987). "The codon adaptation index-a measure of directional synonymous codon usage bias, and its potential applications". Nucleic Acids Research. 15 (3): 1281–1295. doi:10.1093/nar/15.3.1281. ISSN 0305-1048. PMC 340524. PMID 3547335.
- Noble, Peter A.; Citek, Robert W.; Ogunseitan, Oladele A. (April 1998). "Tetranucleotide frequencies in microbial genomes". Electrophoresis. 19 (4): 528–535. doi:10.1002/elps.1150190412. ISSN 0173-0835. PMID 9588798. S2CID 9539686.
- Nagarajan, Niranjan; Pop, Mihai (2013). "Sequence assembly demystified". Nature Reviews Genetics. 14 (3): 157–167. doi:10.1038/nrg3367. ISSN 1471-0056. PMID 23358380. S2CID 3519991.
- Li; et al. (2010). "De novo assembly of human genomes with massively parallel short read sequencing". Genome Research. 20 (2): 265–272. doi:10.1101/gr.097261.109. PMC 2813482. PMID 20019144.
- Compeau, P.; Pevzner, P.; Teslar, G. (2011). "How to apply de Bruijn graphs to genome assembly". Nature Biotechnology. 29 (11): 987–991. doi:10.1038/nbt.2023. PMC 5531759. PMID 22068540.
- Phillippy, Schatz, Pop (2008). "Genome assembly forensics: finding the elusive mis-assembly". Bioinformatics. 9 (3): R55. doi:10.1186/gb-2008-9-3-r55. PMC 2397507. PMID 18341692.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Delmont, Eren (2016). "Identifying contamination with advanced visualization and analysis practices: metagenomic approaches for eukaryotic genome assemblies". PeerJ. 4: e1839. doi:10.7717/peerj.1839. PMC 4824900. PMID 27069789.
- Bemm; et al. (2016). "Genome of a tardigrade: Horizontal gene transfer or bacterial contamination?". Proceedings of the National Academy of Sciences. 113 (22): E3054–E3056. Bibcode:2016PNAS..113E3054B. doi:10.1073/pnas.1525116113. PMC 4896698. PMID 27173902.
- Zerbino, Daniel R.; Birney, Ewan (2008). "Velvet: algorithms for de novo short read assembly using de Bruijn graphs". Genome Research. 18 (5): 821–829. doi:10.1101/gr.074492.107. PMC 2336801. PMID 18349386.
- Goodur, Haswanee D.; Ramtohul, Vyasanand; Baichoo, Shakuntala (2012-11-11). "GIDT — A tool for the identification and visualization of genomic islands in prokaryotic organisms". 2012 IEEE 12th International Conference on Bioinformatics & Bioengineering (BIBE). pp. 58–63. doi:10.1109/bibe.2012.6399707. ISBN 978-1-4673-4358-9. S2CID 6368495.
- Jaron, K. S.; Moravec, J. C.; Martinkova, N. (2014-04-15). "SigHunt: horizontal gene transfer finder optimized for eukaryotic genomes". Bioinformatics. 30 (8): 1081–1086. doi:10.1093/bioinformatics/btt727. ISSN 1367-4803. PMID 24371153.
- Starr, M. P.; Mandel, M. (1969-04-01). "DNA Base Composition and Taxonomy of Phytopathogenic and Other Enterobacteria". Journal of General Microbiology. 56 (1): 113–123. doi:10.1099/00221287-56-1-113. ISSN 0022-1287. PMID 5787000.
- Moore, W. E. C.; Stackebrandt, E.; Kandler, O.; Colwell, R. R.; Krichevsky, M. I.; Truper, H. G.; Murray, R. G. E.; Wayne, L. G.; Grimont, P. A. D. (1987-10-01). "Report of the Ad Hoc Committee on Reconciliation of Approaches to Bacterial Systematics". International Journal of Systematic and Evolutionary Microbiology. 37 (4): 463–464. doi:10.1099/00207713-37-4-463. ISSN 1466-5026.
- Patro, Mount, Kingsford (2014). "Sailfish enables alignment-free isoform quantification from RNA-seq reads using lightweight algorithms". Nature Biotechnology. 32 (5): 462–464. arXiv:1308.3700. doi:10.1038/nbt.2862. PMC 4077321. PMID 24752080.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Navarro-Gomez; et al. (2015). "Phy-Mer: a novel alignment-free and reference-independent mitochondrial haplogroup classifier". Bioinformatics. 31 (8): 1310–1312. doi:10.1093/bioinformatics/btu825. PMC 4393525. PMID 25505086.
- Wang, Rong; Xu, Yong; Liu, Bin (2016). "Recombination spot identification Based on gapped k-mers". Scientific Reports. 6 (1): 23934. Bibcode:2016NatSR...623934W. doi:10.1038/srep23934. ISSN 2045-2322. PMC 4814916. PMID 27030570.
- Hozza, Michal; Vinař, Tomáš; Brejová, Broňa (2015), Iliopoulos, Costas; Puglisi, Simon; Yilmaz, Emine (eds.), "How Big is that Genome? Estimating Genome Size and Coverage from k-mer Abundance Spectra", String Processing and Information Retrieval, Springer International Publishing, vol. 9309, pp. 199–209, doi:10.1007/978-3-319-23826-5_20, ISBN 9783319238258
- Lamichhaney, Sangeet; Fan, Guangyi; Widemo, Fredrik; Gunnarsson, Ulrika; Thalmann, Doreen Schwochow; Hoeppner, Marc P; Kerje, Susanne; Gustafson, Ulla; Shi, Chengcheng (2016). "Structural genomic changes underlie alternative reproductive strategies in the ruff (Philomachus pugnax)". Nature Genetics. 48 (1): 84–88. doi:10.1038/ng.3430. ISSN 1061-4036. PMID 26569123.
- Chae; et al. (2013). "Comparative analysis using K-mer and K-flank patterns provides evidence for CpG island sequence evolution in mammalian genomes". Nucleic Acids Research. 41 (9): 4783–4791. doi:10.1093/nar/gkt144. PMC 3643570. PMID 23519616.
- Mohamed Hashim, Abdullah (2015). "Rare k-mer DNA: Identification of sequence motifs and prediction of CpG island and promoter". Journal of Theoretical Biology. 387: 88–100. Bibcode:2015JThBi.387...88M. doi:10.1016/j.jtbi.2015.09.014. PMID 26427337.
- Price, Jones, Pevzner (2005). "De novo identification of repeat families in large genomes". Bioinformatics. 21(supp 1): i351–8. doi:10.1093/bioinformatics/bti1018. PMID 15961478.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Meher, Prabina Kumar; Sahu, Tanmaya Kumar; Rao, A.R. (2016). "Identification of species based on DNA barcode using k-mer feature vector and Random forest classifier". Gene. 592 (2): 316–324. doi:10.1016/j.gene.2016.07.010. PMID 27393648.
- Newburger, Bulyk (2009). "UniPROBE: an online database of protein binding microarray data on protein–DNA interactions". Nucleic Acids Research. 37(supp 1) (Database issue): D77–82. doi:10.1093/nar/gkn660. PMC 2686578. PMID 18842628.
- Nordstrom; et al. (2013). "Mutation identification by direct comparison of whole-genome sequencing data from mutant and wild-type individuals using k-mers". Nature Biotechnology. 31 (4): 325–330. doi:10.1038/nbt.2515. PMID 23475072.
- Zhu, Jianfeng; Zheng, Wei-Mou (2014). "Self-organizing approach for meta-genomes". Computational Biology and Chemistry. 53: 118–124. doi:10.1016/j.compbiolchem.2014.08.016. PMID 25213854.
- Dubinkina; Ischenko; Ulyantsev; Tyakht; Alexeev (2016). "Assessment of k-mer spectrum applicability for metagenomic dissimilarity analysis". BMC Bioinformatics. 17: 38. doi:10.1186/s12859-015-0875-7. PMC 4715287. PMID 26774270.
- Teeling, H; Waldmann, J; Lombardot, T; Bauer, M; Glöckner, F (2004). "TETRA: a web-service and a stand-alone program for the analysis and comparison of tetranucleotide usage patterns in DNA sequences". BMC Bioinformatics. 5: 163. doi:10.1186/1471-2105-5-163. PMC 529438. PMID 15507136.
- Chatterji, Sourav; Yamazaki, Ichitaro; Bai, Zhaojun; Eisen, Jonathan A. (2008), Vingron, Martin; Wong, Limsoon (eds.), "CompostBin: A DNA Composition-Based Algorithm for Binning Environmental Shotgun Reads", Research in Computational Molecular Biology, Springer Berlin Heidelberg, vol. 4955, pp. 17–28, arXiv:0708.3098, doi:10.1007/978-3-540-78839-3_3, ISBN 9783540788386, S2CID 7832512
- Zheng, Hao; Wu, Hongwei (2010). "Short Prokaryotic DNA Fragment Binning Using a Hierarchical Classifier Based on Linear Discriminant Analysis and Principal Component Analysis". Journal of Bioinformatics and Computational Biology. 08 (6): 995–1011. doi:10.1142/S0219720010005051. ISSN 0219-7200. PMID 21121023.
- McHardy, Alice Carolyn; Martín, Héctor García; Tsirigos, Aristotelis; Hugenholtz, Philip; Rigoutsos, Isidore (2007). "Accurate phylogenetic classification of variable-length DNA fragments". Nature Methods. 4 (1): 63–72. doi:10.1038/nmeth976. ISSN 1548-7091. PMID 17179938. S2CID 28797816.
- Ounit, Rachid; Wanamaker, Steve; Close, Timothy J; Lonardi, Stefano (2015). "CLARK: fast and accurate classification of metagenomic and genomic sequences using discriminative k-mers". BMC Genomics. 16 (1): 236. doi:10.1186/s12864-015-1419-2. ISSN 1471-2164. PMC 4428112. PMID 25879410.
- Diaz, Naryttza N; Krause, Lutz; Goesmann, Alexander; Niehaus, Karsten; Nattkemper, Tim W (2009). "TACOA – Taxonomic classification of environmental genomic fragments using a kernelized nearest neighbor approach". BMC Bioinformatics. 10 (1): 56. doi:10.1186/1471-2105-10-56. ISSN 1471-2105. PMC 2653487. PMID 19210774.
- Fiannaca, Antonino; La Paglia, Laura; La Rosa, Massimo; Lo Bosco, Giosue’; Renda, Giovanni; Rizzo, Riccardo; Gaglio, Salvatore; Urso, Alfonso (2018). "Deep learning models for bacteria taxonomic classification of metagenomic data". BMC Bioinformatics. 19 (S7): 198. doi:10.1186/s12859-018-2182-6. ISSN 1471-2105. PMC 6069770. PMID 30066629.
- Zhu, Zheng (2014). "Self-organizing approach for meta-genomes". Computational Biology and Chemistry. 53: 118–124. doi:10.1016/j.compbiolchem.2014.08.016. PMID 25213854.
- Lu, Jennifer; Breitwieser, Florian P.; Thielen, Peter; Salzberg, Steven L. (2017-01-02). "Bracken: estimating species abundance in metagenomics data". PeerJ Computer Science. 3: e104. doi:10.7717/peerj-cs.104. ISSN 2376-5992.
- Wood, Derrick E; Salzberg, Steven L (2014). "Kraken: ultrafast metagenomic sequence classification using exact alignments". Genome Biology. 15 (3): R46. doi:10.1186/gb-2014-15-3-r46. ISSN 1465-6906. PMC 4053813. PMID 24580807.
- Rosen, Gail; Garbarine, Elaine; Caseiro, Diamantino; Polikar, Robi; Sokhansanj, Bahrad (2008). "Metagenome Fragment Classification Using -Mer Frequency Profiles". Advances in Bioinformatics. 2008: 205969. doi:10.1155/2008/205969. ISSN 1687-8027. PMC 2777009. PMID 19956701.
- Wang, Ying; Fu, Lei; Ren, Jie; Yu, Zhaoxia; Chen, Ting; Sun, Fengzhu (2018-05-03). "Identifying Group-Specific Sequences for Microbial Communities Using Long k-mer Sequence Signatures". Frontiers in Microbiology. 9: 872. doi:10.3389/fmicb.2018.00872. ISSN 1664-302X. PMC 5943621. PMID 29774017.
- Al-Saif, Maher; Khabar, Khalid SA (2012). "UU/UA Dinucleotide Frequency Reduction in Coding Regions Results in Increased mRNA Stability and Protein Expression". Molecular Therapy. 20 (5): 954–959. doi:10.1038/mt.2012.29. PMC 3345983. PMID 22434136.
- Trinh, R; Gurbaxani, B; Morrison, SL; Seyfzadeh, M (2004). "Optimization of codon pair use within the (GGGGS)3 linker sequence results in enhanced protein expression". Molecular Immunology. 40 (10): 717–722. doi:10.1016/j.molimm.2003.08.006. PMID 14644097. S2CID 36734007.
- Shen, Sam H.; Stauft, Charles B.; Gorbatsevych, Oleksandr; Song, Yutong; Ward, Charles B.; Yurovsky, Alisa; Mueller, Steffen; Futcher, Bruce; Wimmer, Eckard (2015-04-14). "Large-scale recoding of an arbovirus genome to rebalance its insect versus mammalian preference". Proceedings of the National Academy of Sciences. 112 (15): 4749–4754. Bibcode:2015PNAS..112.4749S. doi:10.1073/pnas.1502864112. ISSN 0027-8424. PMC 4403163. PMID 25825721.
- Kaplan, Bryan S.; Souza, Carine K.; Gauger, Phillip C.; Stauft, Charles B.; Robert Coleman, J.; Mueller, Steffen; Vincent, Amy L. (2018). "Vaccination of pigs with a codon-pair bias de-optimized live attenuated influenza vaccine protects from homologous challenge". Vaccine. 36 (8): 1101–1107. doi:10.1016/j.vaccine.2018.01.027. PMID 29366707.
- Eschke, Kathrin; Trimpert, Jakob; Osterrieder, Nikolaus; Kunec, Dusan (2018-01-29). Mocarski, Edward (ed.). "Attenuation of a very virulent Marek's disease herpesvirus (MDV) by codon pair bias deoptimization". PLOS Pathogens. 14 (1): e1006857. doi:10.1371/journal.ppat.1006857. ISSN 1553-7374. PMC 5805365. PMID 29377958.
- Kunec, Dusan; Osterrieder, Nikolaus (2016). "Codon Pair Bias Is a Direct Consequence of Dinucleotide Bias". Cell Reports. 14 (1): 55–67. doi:10.1016/j.celrep.2015.12.011. PMID 26725119.
- Tulloch, Fiona; Atkinson, Nicky J; Evans, David J; Ryan, Martin D; Simmonds, Peter (2014-12-09). "RNA virus attenuation by codon pair deoptimisation is an artefact of increases in CpG/UpA dinucleotide frequencies". eLife. 3: e04531. doi:10.7554/eLife.04531. ISSN 2050-084X. PMC 4383024. PMID 25490153.
- Marçais, Guillaume; Kingsford, Carl (2011-03-15). "A fast, lock-free approach for efficient parallel counting of occurrences of k-mers". Bioinformatics. 27 (6): 764–770. doi:10.1093/bioinformatics/btr011. ISSN 1460-2059. PMC 3051319. PMID 21217122.
- Deorowicz, Sebastian; Kokot, Marek; Grabowski, Szymon; Debudaj-Grabysz, Agnieszka (2015-05-15). "KMC 2: fast and resource-frugal k-mer counting". Bioinformatics. 31 (10): 1569–1576. arXiv:1407.1507. doi:10.1093/bioinformatics/btv022. ISSN 1460-2059. PMID 25609798.
- Erbert, Marius; Rechner, Steffen; Müller-Hannemann, Matthias (2017). "Gerbil: a fast and memory-efficient k-mer counter with GPU-support". Algorithms for Molecular Biology. 12 (1): 9. doi:10.1186/s13015-017-0097-9. ISSN 1748-7188. PMC 5374613. PMID 28373894.