Kaniadakis Weibull distribution
The Kaniadakis Weibull distribution (or κ-Weibull distribution) is a probability distribution arising as a generalization of the Weibull distribution.[1][2] It is one example of a Kaniadakis κ-distribution. The κ-Weibull distribution has been adopted successfully for describing a wide variety of complex systems in seismology, economy, epidemiology, among many others.
|
Probability density function 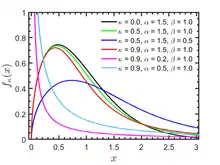 | |||
|
Cumulative distribution function 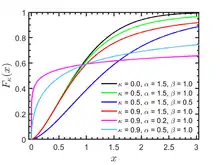 | |||
| Parameters |
rate shape (real) rate (real) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Quantile | |||
| Median | |||
| Mode | |||
| Method of Moments | |||
Definitions
Probability density function
The Kaniadakis κ-Weibull distribution is exhibits power-law right tails, and it has the following probability density function:[3]
valid for , where is the entropic index associated with the Kaniadakis entropy, is the scale parameter, and is the shape parameter or Weibull modulus.
The Weibull distribution is recovered as
Cumulative distribution function
The cumulative distribution function of κ-Weibull distribution is given by
valid for . The cumulative Weibull distribution is recovered in the classical limit .
Survival distribution and hazard functions
The survival distribution function of κ-Weibull distribution is given by
valid for . The survival Weibull distribution is recovered in the classical limit .
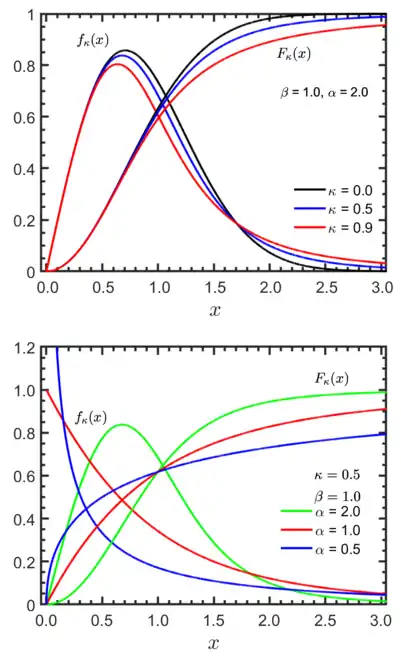
The hazard function of the κ-Weibull distribution is obtained through the solution of the κ-rate equation:
with , where is the hazard function:
The cumulative κ-Weibull distribution is related to the κ-hazard function by the following expression:
where
is the cumulative κ-hazard function. The cumulative hazard function of the Weibull distribution is recovered in the classical limit : .
Properties
Moments, median and mode
The κ-Weibull distribution has moment of order given by
The median and the mode are:
Related distributions
- The κ-Weibull distribution is a generalization of:
- κ-Exponential distribution of type II, when ;
- Exponential distribution when and .
- A κ-Weibull distribution corresponds to a κ-deformed Rayleigh distribution when and a Rayleigh distribution when and .
Applications
The κ-Weibull distribution has been applied in several areas, such as:
- In economy, for analyzing personal income models, in order to accurately describing simultaneously the income distribution among the richest part and the great majority of the population.[1][4][5]
- In seismology, the κ-Weibull represents the statistical distribution of magnitude of the earthquakes distributed across the Earth, generalizing the Gutenberg–Richter law,[6] and the interval distributions of seismic data, modeling extreme-event return intervals.[7][8]
- In epidemiology, the κ-Weibull distribution presents a universal feature for epidemiological analysis.[9]
See also
References
- Clementi, F.; Gallegati, M.; Kaniadakis, G. (2007). "κ-generalized statistics in personal income distribution". The European Physical Journal B. 57 (2): 187–193. arXiv:physics/0607293. Bibcode:2007EPJB...57..187C. doi:10.1140/epjb/e2007-00120-9. ISSN 1434-6028. S2CID 15777288.
- Clementi, F.; Di Matteo, T.; Gallegati, M.; Kaniadakis, G. (2008). "The -generalized distribution: A new descriptive model for the size distribution of incomes". Physica A: Statistical Mechanics and Its Applications. 387 (13): 3201–3208. arXiv:0710.3645. doi:10.1016/j.physa.2008.01.109. S2CID 2590064.
- Kaniadakis, G. (2021-01-01). "New power-law tailed distributions emerging in κ-statistics (a)". Europhysics Letters. 133 (1): 10002. arXiv:2203.01743. Bibcode:2021EL....13310002K. doi:10.1209/0295-5075/133/10002. ISSN 0295-5075. S2CID 234144356.
- Clementi, Fabio; Gallegati, Mauro; Kaniadakis, Giorgio (October 2010). "A model of personal income distribution with application to Italian data". Empirical Economics. 39 (2): 559–591. doi:10.1007/s00181-009-0318-2. ISSN 0377-7332. S2CID 154273794.
- Clementi, F; Gallegati, M; Kaniadakis, G (2012-12-06). "A generalized statistical model for the size distribution of wealth". Journal of Statistical Mechanics: Theory and Experiment. 2012 (12): P12006. arXiv:1209.4787. Bibcode:2012JSMTE..12..006C. doi:10.1088/1742-5468/2012/12/P12006. ISSN 1742-5468. S2CID 18961951.
- da Silva, Sérgio Luiz E.F. (2021). "κ -generalised Gutenberg–Richter law and the self-similarity of earthquakes". Chaos, Solitons & Fractals. 143: 110622. Bibcode:2021CSF...14310622D. doi:10.1016/j.chaos.2020.110622. S2CID 234063959.
- Hristopulos, Dionissios T.; Petrakis, Manolis P.; Kaniadakis, Giorgio (2014-05-28). "Finite-size effects on return interval distributions for weakest-link-scaling systems". Physical Review E. 89 (5): 052142. arXiv:1308.1881. Bibcode:2014PhRvE..89e2142H. doi:10.1103/PhysRevE.89.052142. ISSN 1539-3755. PMID 25353774. S2CID 22310350.
- Hristopulos, Dionissios; Petrakis, Manolis; Kaniadakis, Giorgio (2015-03-09). "Weakest-Link Scaling and Extreme Events in Finite-Sized Systems". Entropy. 17 (3): 1103–1122. Bibcode:2015Entrp..17.1103H. doi:10.3390/e17031103. ISSN 1099-4300.
- Kaniadakis, Giorgio; Baldi, Mauro M.; Deisboeck, Thomas S.; Grisolia, Giulia; Hristopulos, Dionissios T.; Scarfone, Antonio M.; Sparavigna, Amelia; Wada, Tatsuaki; Lucia, Umberto (2020). "The κ-statistics approach to epidemiology". Scientific Reports. 10 (1): 19949. Bibcode:2020NatSR..1019949K. doi:10.1038/s41598-020-76673-3. ISSN 2045-2322. PMC 7673996. PMID 33203913.