Keyhole problem

The green volume illustrates visible space limited by the keyhole problem. The arrow points to the "keyhole" as unviewable sky volume.

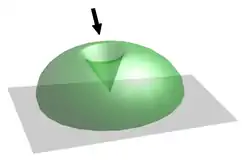
To track celestial objects as they move across the sky, these systems usually rotate on two axes. Often, a tilting mechanism (elevation) is mounted upon a panning base (azimuth). To cover the complete hemisphere of visible sky, a telescope gimbal can have a 360-degree azimuth range and a 0- to 90-degree elevation range. To visualize this shape, imagine drawing a quarter circle spanning from the horizon to directly above you and revolving it around the vertical axis. If, on the other hand, the gimbal has a range from 0 to slightly less than 90 degrees elevation, the telescope is unable to see a region of sky.

A variation on the keyhole problem involves defining behavior for gimbals with full-circle azimuth range, and at least 90-degree but less than 180-degree elevation range. Imagine a satellite on an orbital path that crosses directly overhead. If the gimbal tilts to track the object from the horizon but must stop at 90 degrees, the entire telescope must pan 180 degrees to follow the object from zenith down to the opposite horizon.

When there is a full-circle azimuth range and full 180-degree elevation range, all points can be reached without the need for an instantaneous 180-degree rotation of the azimuth. Passing directly through the zenith can be done smoothly. However, tracking an object that passes near (but not directly through) the zenith will require the azimuth to rotate increasingly faster as the zenith is approached. This will pose practical issues for a physical system with a motor than can only move the azimuthal axis at a limited rate and acceleration. And so the keyhole problem is a fundamental issue for any real azimuth-elevation type tracking system, even if designed to reach the whole range of half-hemispherical angles.

These are often-encountered difficulties in creating smooth automated tracking algorithms.