Kinoshita–Terasaka knot
In knot theory, the Kinoshita–Terasaka knot is a particular prime knot. It has 11 crossings.[1] The Kinoshita–Terasaka knot has a variety of interesting mathematical properties.[2] It is related by mutation to the Conway knot,[3] with which it shares a Jones polynomial. It has the same Alexander polynomial as the unknot.[4]
| Kinoshita–Terasaka knot | |
|---|---|
| Crossing no. | 11 |
| Genus | 2 |
| Thistlethwaite | 11n42 |
| Other | |
| prime, prime, slice | |
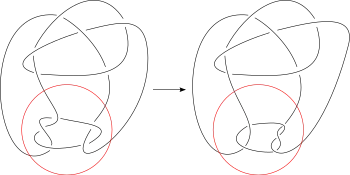
The prime Kinoshita–Terasaka knot (11n42) (left) and the prime Conway knot (11n34) (right) showing how they are related by mutation
References
- Weisstein, Eric W. "Conway's Knot". mathworld.wolfram.com. Retrieved 2020-05-19.
- Tillmann, Stephan (June 2000). "On the Kinoshita-Terasaka knot and generalised Conway mutation" (PDF). Journal of Knot Theory and Its Ramifications. 09 (4): 557–575. doi:10.1142/S0218216500000311. ISSN 0218-2165.
- Chmutov, S.V. (2007). "Mutant Knots" (PDF). people.math.osu.edu. Archived from the original (PDF) on 2020-06-12.
- Boi, Luciano (2 November 2005). Geometries of Nature, Living Systems and Human Cognition: New Interactions of Mathematics with Natural Sciences and Humanities. ISBN 9789814479455.
External links
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.