Kobon triangle problem

Saburo Tamura proved that the number of nonoverlapping triangles realizable by ${\displaystyle k}$ lines is at most ${\displaystyle \lfloor k(k-2)/3\rfloor }$. G. Clément and J. Bader proved more strongly that this bound cannot be achieved when ${\displaystyle k}$ is congruent to 0 or 2 (mod 6).[2] The maximum number of triangles is therefore at most one less in these cases. The same bounds can be equivalently stated, without use of the floor function, as:

$${\displaystyle {\begin{cases}{\frac {1}{3}}k(k-2)&{\text{when }}k\equiv 3,5{\pmod {6}};\\{\frac {1}{3}}(k+1)(k-3)&{\text{when }}k\equiv 0,2{\pmod {6}};\\{\frac {1}{3}}(k^{2}-2k-2)&{\text{when }}k\equiv 1,4{\pmod {6}}.\end{cases}}}$$

Solutions yielding this number of triangles are known when ${\displaystyle k}$ is 3, 4, 5, 6, 7, 8, 9, 13, 15 or 17.[3] For k = 10, 11 and 12, the best solutions known reach a number of triangles one less than the upper bound.

Given an optimal solution with k₀ > 3 lines, other Kobon triangle solution numbers can be found for all k_i-values where

$${\displaystyle k_{n+1}=2\cdot k_{n}-1,}$$

by using the procedure by D. Forge and J. L. Ramirez Alfonsin.[1] For example, the solution for k₀ = 5 leads to the maximal number of nonoverlapping triangles for k = 5, 9, 17, 33, 65, ....

• 
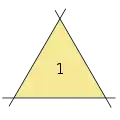  3 lines, 1 triangle
• 
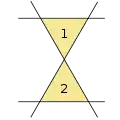  4 lines, 2 triangles
• 
  5 lines, 5 triangles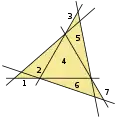
• 
  6 lines, 7 triangles
• 
  7 lines, 11 triangles

• Roberts's triangle theorem, on the minimum number of triangles that ${\displaystyle n}$ lines can form

• Johannes Bader, "Kobon Triangles"