Kolmogorov's criterion
In probability theory, Kolmogorov's criterion, named after Andrey Kolmogorov, is a theorem giving a necessary and sufficient condition for a Markov chain or continuous-time Markov chain to be stochastically identical to its time-reversed version.
Discrete-time Markov chains
The theorem states that an irreducible, positive recurrent, aperiodic Markov chain with transition matrix P is reversible if and only if its stationary Markov chain satisfies[1]
for all finite sequences of states
Here pij are components of the transition matrix P, and S is the state space of the chain.
Example
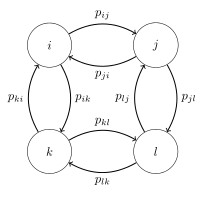
Consider this figure depicting a section of a Markov chain with states i, j, k and l and the corresponding transition probabilities. Here Kolmogorov's criterion implies that the product of probabilities when traversing through any closed loop must be equal, so the product around the loop i to j to l to k returning to i must be equal to the loop the other way round,
Proof
Let be the Markov chain and denote by its stationary distribution (such exists since the chain is positive recurrent).
If the chain is reversible, the equality follows from the relation .
Now assume that the equality is fulfilled. Fix states and . Then
- .
Now sum both sides of the last equality for all possible ordered choices of states . Thus we obtain so . Send to on the left side of the last. From the properties of the chain follows that , hence which shows that the chain is reversible.
Continuous-time Markov chains
The theorem states that a continuous-time Markov chain with transition rate matrix Q is, under any invariant probability vector, reversible if and only if its transition probabilities satisfy[1]
for all finite sequences of states
The proof for continuous-time Markov chains follows in the same way as the proof for discrete-time Markov chains.
References
- Kelly, Frank P. (1979). Reversibility and Stochastic Networks (PDF). Wiley, Chichester. pp. 21–25.