Brillouin and Langevin functions

The Brillouin function[1][2] is a special function defined by the following equation:

${\displaystyle B_{J}(x)={\frac {2J+1}{2J}}\coth \left({\frac {2J+1}{2J}}x\right)-{\frac {1}{2J}}\coth \left({\frac {1}{2J}}x\right)}$

The function is usually applied (see below) in the context where ${\displaystyle x}$ is a real variable and ${\displaystyle J}$ is a positive integer or half-integer. In this case, the function varies from -1 to 1, approaching +1 as ${\displaystyle x\to +\infty }$ and -1 as ${\displaystyle x\to -\infty }$.

The function is best known for arising in the calculation of the magnetization of an ideal paramagnet. In particular, it describes the dependency of the magnetization ${\displaystyle M}$ on the applied magnetic field ${\displaystyle B}$ and the total angular momentum quantum number J of the microscopic magnetic moments of the material. The magnetization is given by:[1]

${\displaystyle M=Ng\mu _{\rm {B}}JB_{J}(x)}$

where

• ${\displaystyle N}$ is the number of atoms per unit volume,
• ${\displaystyle g}$ the g-factor,
• ${\displaystyle \mu _{\rm {B}}}$ the Bohr magneton,
• ${\displaystyle x}$ is the ratio of the Zeeman energy of the magnetic moment in the external field to the thermal energy ${\displaystyle k_{\rm {B}}T}$:[1]

${\displaystyle x=J{\frac {g\mu _{\rm {B}}B}{k_{\rm {B}}T}}}$

• ${\displaystyle k_{\rm {B}}}$ is the Boltzmann constant and ${\displaystyle T}$ the temperature.

Note that in the SI system of units ${\displaystyle B}$ given in Tesla stands for the magnetic field, ${\displaystyle B=\mu _{0}H}$, where ${\displaystyle H}$ is the auxiliary magnetic field given in A/m and ${\displaystyle \mu _{0}}$ is the permeability of vacuum.

Click "show" to see a derivation of this law:

A derivation of this law describing the magnetization of an ideal paramagnet is as follows.[1] Let z be the direction of the magnetic field. The z-component of the angular momentum of each magnetic moment (a.k.a. the azimuthal quantum number) can take on one of the 2J+1 possible values -J,-J+1,...,+J. Each of these has a different energy, due to the external field B: The energy associated with quantum number m is ${\displaystyle E_{m}=-mg\mu _{\rm {B}}B=-k_{\rm {B}}Txm/J}$ (where g is the g-factor, μB is the Bohr magneton, and x is as defined in the text above). The relative probability of each of these is given by the Boltzmann factor: ${\displaystyle P(m)=e^{-E_{m}/(k_{\rm {B}}T)}/Z=e^{xm/J}/Z}$ where Z (the partition function) is a normalization constant such that the probabilities sum to unity. Calculating Z, the result is: ${\displaystyle P(m)=e^{xm/J}/\left(\sum _{m'=-J}^{J}e^{xm'/J}\right)}$. All told, the expectation value of the azimuthal quantum number m is ${\displaystyle \langle m\rangle =(-J)\times P(-J)+\cdots +J\times P(J)=\left(\sum _{m=-J}^{J}me^{xm/J}\right)/\left(\sum _{m=-J}^{J}e^{xm/J}\right)}$. The denominator is a geometric series and the numerator is a type of arithmetico–geometric series, so the series can be explicitly summed. After some algebra, the result turns out to be ${\displaystyle \langle m\rangle =JB_{J}(x)}$ With N magnetic moments per unit volume, the magnetization density is ${\displaystyle M=Ng\mu _{\rm {B}}\langle m\rangle =NgJ\mu _{\rm {B}}B_{J}(x)}$.

Takacs[3] proposed the following approximation to the inverse of the Brillouin function:

${\displaystyle B_{J}(x)^{-1}={\frac {axJ^{2}}{1-bx^{2}}}}$

where the constants ${\displaystyle a}$ and ${\displaystyle b}$ are defined to be

${\displaystyle a={\frac {0.5(1+2J)(1-0.055)}{(J-0.27)2J}}+{\frac {0.1}{J^{2}}}}$

${\displaystyle b=0.8}$

Langevin function (blue line), compared with ${\displaystyle \tanh(x/3)}$ (magenta line).

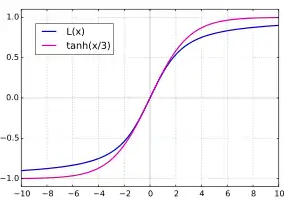
In the classical limit, the moments can be continuously aligned in the field and ${\displaystyle J}$ can assume all values (${\displaystyle J\to \infty }$). The Brillouin function is then simplified into the Langevin function, named after Paul Langevin:

${\displaystyle L(x)=\coth(x)-{\frac {1}{x}}}$

For small values of x, the Langevin function can be approximated by a truncation of its Taylor series:

${\displaystyle L(x)={\tfrac {1}{3}}x-{\tfrac {1}{45}}x^{3}+{\tfrac {2}{945}}x^{5}-{\tfrac {1}{4725}}x^{7}+\dots }$

An alternative, better behaved approximation can be derived from the Lambert's continued fraction expansion of tanh(x):

${\displaystyle L(x)={\frac {x}{3+{\tfrac {x^{2}}{5+{\tfrac {x^{2}}{7+{\tfrac {x^{2}}{9+\ldots }}}}}}}}}$

For small enough x, both approximations are numerically better than a direct evaluation of the actual analytical expression, since the latter suffers from catastrophic cancellation for ${\displaystyle x\approx 0}$ where ${\displaystyle \coth(x)\approx 1/x}$.

The inverse Langevin function L⁻¹(x) is defined on the open interval (−1, 1). For small values of x, it can be approximated by a truncation of its Taylor series[4]

${\displaystyle L^{-1}(x)=3x+{\tfrac {9}{5}}x^{3}+{\tfrac {297}{175}}x^{5}+{\tfrac {1539}{875}}x^{7}+\dots }$

and by the Padé approximant

${\displaystyle L^{-1}(x)=3x{\frac {35-12x^{2}}{35-33x^{2}}}+O(x^{7}).}$

Graphs of relative error for x ∈ [0, 1) for Cohen and Jedynak approximations

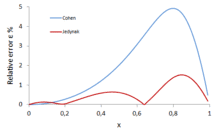
Since this function has no closed form, it is useful to have approximations valid for arbitrary values of x. One popular approximation, valid on the whole range (−1, 1), has been published by A. Cohen:[5]

${\displaystyle L^{-1}(x)\approx x{\frac {3-x^{2}}{1-x^{2}}}.}$

This has a maximum relative error of 4.9% at the vicinity of x = ±0.8. Greater accuracy can be achieved by using the formula given by R. Jedynak:[6]

${\displaystyle L^{-1}(x)\approx x{\frac {3.0-2.6x+0.7x^{2}}{(1-x)(1+0.1x)}},}$

valid for x ≥ 0. The maximal relative error for this approximation is 1.5% at the vicinity of x = 0.85. Even greater accuracy can be achieved by using the formula given by M. Kröger:[7]

${\displaystyle L^{-1}(x)\approx {\frac {3x-x(6x^{2}+x^{4}-2x^{6})/5}{1-x^{2}}}}$

The maximal relative error for this approximation is less than 0.28%. More accurate approximation was reported by R. Petrosyan:[8]

${\displaystyle L^{-1}(x)\approx 3x+{\frac {x^{2}}{5}}\sin \left({\frac {7x}{2}}\right)+{\frac {x^{3}}{1-x}},}$

valid for x ≥ 0. The maximal relative error for the above formula is less than 0.18%.[8]

New approximation given by R. Jedynak,[9] is the best reported approximant at complexity 11:

${\displaystyle L^{-1}(x)\approx {\frac {x(3-1.00651x^{2}-0.962251x^{4}+1.47353x^{6}-0.48953x^{8})}{(1-x)(1+1.01524x)}},}$

valid for x ≥ 0. Its maximum relative error is less than 0.076%.[9]

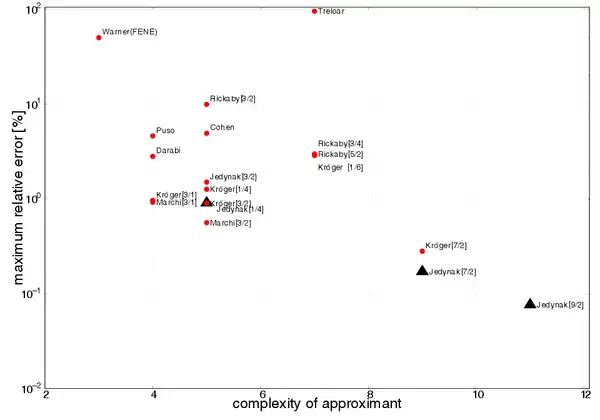
Current state-of-the-art diagram of the approximants to the inverse Langevin function presents the figure below. It is valid for the rational/Padé approximants,[7][9]

Current state-of-the-art diagram of the approximants to the inverse Langevin function,[7][9]

A recently published paper by R. Jedynak,[10] provides a series of the optimal approximants to the inverse Langevin function. The table below reports the results with correct asymptotic behaviors,.[7][9][10]

Comparison of relative errors for the different optimal rational approximations, which were computed with constraints (Appendix 8 Table 1)[10]

Complexity	Optimal approximation	Maximum relative error [%]
3	${\displaystyle R_{2,1}(y)={\frac {-2y^{2}+3y}{1-y}}}$	13
4	${\displaystyle R_{3,1}(y)={\frac {0.88y^{3}-2.88y^{2}+3y}{1-y}}}$	0.95
5	${\displaystyle R_{3,2}(y)={\frac {1.1571y^{3}-3.3533y^{2}+3y}{(1-y)(1-0.1962y)}}}$	0.56
6	${\displaystyle R_{5,1}(y)={\frac {0.756y^{5}-1.383y^{4}+1.5733y^{3}-2.9463y^{2}+3y}{1-y}}}$	0.16
7	${\displaystyle R_{3,4}(y)={\frac {2.14234y^{3}-4.22785y^{2}+3y}{(1-y)\left(0.71716y^{3}-0.41103y^{2}-0.39165y+1\right)}}}$	0.082

Also recently, an efficient near-machine precision approximant, based on spline interpolations, has been proposed by Benítez and Montáns,[11] where Matlab code is also given to generate the spline-based approximant and to compare many of the previously proposed approximants in all the function domain.

When ${\displaystyle x\ll 1}$ i.e. when ${\displaystyle \mu _{\rm {B}}B/k_{\rm {B}}T}$ is small, the expression of the magnetization can be approximated by the Curie's law:

${\displaystyle M=C\cdot {\frac {B}{T}}}$

where ${\displaystyle C={\frac {Ng^{2}J(J+1)\mu _{\rm {B}}^{2}}{3k_{\rm {B}}}}}$ is a constant. One can note that ${\displaystyle g{\sqrt {J(J+1)}}}$ is the effective number of Bohr magnetons.

When ${\displaystyle x\to \infty }$, the Brillouin function goes to 1. The magnetization saturates with the magnetic moments completely aligned with the applied field:

${\displaystyle M=Ng\mu _{\rm {B}}J}$