Leaky integrator

In mathematics, a leaky integrator equation is a specific differential equation, used to describe a component or system that takes the integral of an input, but gradually leaks a small amount of input over time. It appears commonly in hydraulics, electronics, and neuroscience where it can represent either a single neuron or a local population of neurons.[1]

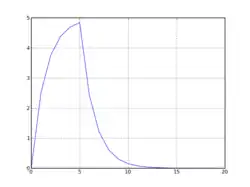
A graph of a solution to a leaky integrator; the input changes at T=5.

Equation

The equation is of the form

dx/dt=-Ax+C

where C is the input and A is the rate of the 'leak'.

General solution

The equation is a nonhomogeneous first-order linear differential equation. For constant C its solution is

x(t)=ke^{-At}+{\frac {C}{A}}

where $k$ is a constant encoding the initial condition.

References

Eliasmith, Anderson, Chris, Charles (2003). Neural Engineering. Cambridge, Massachusetts: MIT Press. pp. 81. ISBN 9780262050715.{{cite book}}: CS1 maint: multiple names: authors list (link)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Eliasmith, Anderson, Chris, Charles (2003). Neural Engineering. Cambridge, Massachusetts: MIT Press. pp. 81. ISBN 9780262050715.{{cite book}}: CS1 maint: multiple names: authors list (link)