List of space groups
There are 230 space groups in three dimensions, given by a number index, and a full name in Hermann–Mauguin notation, and a short name (international short symbol). The long names are given with spaces for readability. The groups each have a point group of the unit cell.
Symbols
In Hermann–Mauguin notation, space groups are named by a symbol combining the point group identifier with the uppercase letters describing the lattice type. Translations within the lattice in the form of screw axes and glide planes are also noted, giving a complete crystallographic space group.
These are the Bravais lattices in three dimensions:
- P primitive
- I body centered (from the German Innenzentriert)
- F face centered (from the German Flächenzentriert)
- A centered on A faces only
- B centered on B faces only
- C centered on C faces only
- R rhombohedral
A reflection plane m within the point groups can be replaced by a glide plane, labeled as a, b, or c depending on which axis the glide is along. There is also the n glide, which is a glide along the half of a diagonal of a face, and the d glide, which is along a quarter of either a face or space diagonal of the unit cell. The d glide is often called the diamond glide plane as it features in the diamond structure.
- , , or : glide translation along half the lattice vector of this face
- : glide translation along half the diagonal of this face
- : glide planes with translation along a quarter of a face diagonal
- : two glides with the same glide plane and translation along two (different) half-lattice vectors.
A gyration point can be replaced by a screw axis denoted by a number, n, where the angle of rotation is . The degree of translation is then added as a subscript showing how far along the axis the translation is, as a portion of the parallel lattice vector. For example, 21 is a 180° (twofold) rotation followed by a translation of ½ of the lattice vector. 31 is a 120° (threefold) rotation followed by a translation of ⅓ of the lattice vector. The possible screw axes are: 21, 31, 32, 41, 42, 43, 61, 62, 63, 64, and 65.
Wherever there is both a rotation or screw axis n and a mirror or glide plane m along the same crystallographic direction, they are represented as a fraction or n/m. For example, 41/a means that the crystallographic axis in question contains both a 41 screw axis as well as a glide plane along a.
In Schoenflies notation, the symbol of a space group is represented by the symbol of corresponding point group with additional superscript. The superscript doesn't give any additional information about symmetry elements of the space group, but is instead related to the order in which Schoenflies derived the space groups. This is sometimes supplemented with a symbol of the form which specifies the Bravais lattice. Here is the lattice system, and is the centering type.[1]
In Fedorov symbol, the type of space group is denoted as s (symmorphic ), h (hemisymmorphic), or a (asymmorphic). The number is related to the order in which Fedorov derived space groups. There are 73 symmorphic, 54 hemisymmorphic, and 103 asymmorphic space groups.
Symmorphic
The 73 symmorphic space groups can be obtained as combination of Bravais lattices with corresponding point group. These groups contain the same symmetry elements as the corresponding point groups, for example, the space groups P4/mmm (, 36s) and I4/mmm (, 37s).
Hemisymmorphic
The 54 hemisymmorphic space groups contain only axial combination of symmetry elements from the corresponding point groups. Hemisymmorphic space groups contain the axial combination 422, which are P4/mcc (, 35h), P4/nbm (, 36h), P4/nnc (, 37h), and I4/mcm (, 38h).
Asymmorphic
The remaining 103 space groups are asymmorphic, for example, those derived from the point group 4/mmm ().
List of triclinic
 |
| Number | Point group | Orbifold | Short name | Full name | Schoenflies | Fedorov | Shubnikov | Fibrifold |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | P1 | P 1 | 1s | ||||
| 2 | 1 | P1 | P 1 | 2s |
List of monoclinic
| Simple (P) | Base (C) |
|---|---|
 |
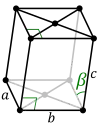 |
| Number | Point group | Orbifold | Short name | Full name(s) | Schoenflies | Fedorov | Shubnikov | Fibrifold (primary) | Fibrifold (secondary) | |
|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 2 | P2 | P 1 2 1 | P 1 1 2 | 3s | |||||
| 4 | P21 | P 1 21 1 | P 1 1 21 | 1a | ||||||
| 5 | C2 | C 1 2 1 | B 1 1 2 | 4s | , | |||||
| 6 | m | Pm | P 1 m 1 | P 1 1 m | 5s | |||||
| 7 | Pc | P 1 c 1 | P 1 1 b | 1h | , | |||||
| 8 | Cm | C 1 m 1 | B 1 1 m | 6s | , | |||||
| 9 | Cc | C 1 c 1 | B 1 1 b | 2h | , | |||||
| 10 | 2/m | P2/m | P 1 2/m 1 | P 1 1 2/m | 7s | |||||
| 11 | P21/m | P 1 21/m 1 | P 1 1 21/m | 2a | ||||||
| 12 | C2/m | C 1 2/m 1 | B 1 1 2/m | 8s | , | |||||
| 13 | P2/c | P 1 2/c 1 | P 1 1 2/b | 3h | , | |||||
| 14 | P21/c | P 1 21/c 1 | P 1 1 21/b | 3a | , | |||||
| 15 | C2/c | C 1 2/c 1 | B 1 1 2/b | 4h | , | |||||
List of orthorhombic
| Simple (P) | Body (I) | Face (F) | Base (A or C) |
|---|---|---|---|
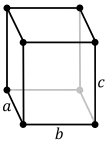 |
 |
 |
 |
| Number | Point group | Orbifold | Short name | Full name | Schoenflies | Fedorov | Shubnikov | Fibrifold (primary) | Fibrifold (secondary) |
|---|---|---|---|---|---|---|---|---|---|
| 16 | 222 | P222 | P 2 2 2 | 9s | |||||
| 17 | P2221 | P 2 2 21 | 4a | ||||||
| 18 | P21212 | P 21 21 2 | 7a | | |||||
| 19 | P212121 | P 21 21 21 | 8a | | |||||
| 20 | C2221 | C 2 2 21 | 5a | ||||||
| 21 | C222 | C 2 2 2 | 10s | ||||||
| 22 | F222 | F 2 2 2 | 12s | ||||||
| 23 | I222 | I 2 2 2 | 11s | ||||||
| 24 | I212121 | I 21 21 21 | 6a | ||||||
| 25 | mm2 | Pmm2 | P m m 2 | 13s | |||||
| 26 | Pmc21 | P m c 21 | 9a | , | |||||
| 27 | Pcc2 | P c c 2 | 5h | ||||||
| 28 | Pma2 | P m a 2 | 6h | , | |||||
| 29 | Pca21 | P c a 21 | 11a | ||||||
| 30 | Pnc2 | P n c 2 | 7h | , | |||||
| 31 | Pmn21 | P m n 21 | 10a | , | |||||
| 32 | Pba2 | P b a 2 | 9h | ||||||
| 33 | Pna21 | P n a 21 | 12a | , | |||||
| 34 | Pnn2 | P n n 2 | 8h | ||||||
| 35 | Cmm2 | C m m 2 | 14s | ||||||
| 36 | Cmc21 | C m c 21 | 13a | , | |||||
| 37 | Ccc2 | C c c 2 | 10h | ||||||
| 38 | Amm2 | A m m 2 | 15s | , | |||||
| 39 | Aem2 | A b m 2 | 11h | , | |||||
| 40 | Ama2 | A m a 2 | 12h | , | |||||
| 41 | Aea2 | A b a 2 | 13h | , | |||||
| 42 | Fmm2 | F m m 2 | 17s | ||||||
| 43 | Fdd2 | F dd2 | 16h | ||||||
| 44 | Imm2 | I m m 2 | 16s | ||||||
| 45 | Iba2 | I b a 2 | 15h | ||||||
| 46 | Ima2 | I m a 2 | 14h | , | |||||
| 47 | Pmmm | P 2/m 2/m 2/m | 18s | ||||||
| 48 | Pnnn | P 2/n 2/n 2/n | 19h | ||||||
| 49 | Pccm | P 2/c 2/c 2/m | 17h | ||||||
| 50 | Pban | P 2/b 2/a 2/n | 18h | ||||||
| 51 | Pmma | P 21/m 2/m 2/a | 14a | , | |||||
| 52 | Pnna | P 2/n 21/n 2/a | 17a | , | |||||
| 53 | Pmna | P 2/m 2/n 21/a | 15a | , | |||||
| 54 | Pcca | P 21/c 2/c 2/a | 16a | , | |||||
| 55 | Pbam | P 21/b 21/a 2/m | 22a | ||||||
| 56 | Pccn | P 21/c 21/c 2/n | 27a | ||||||
| 57 | Pbcm | P 2/b 21/c 21/m | 23a | , | |||||
| 58 | Pnnm | P 21/n 21/n 2/m | 25a | ||||||
| 59 | Pmmn | P 21/m 21/m 2/n | 24a | ||||||
| 60 | Pbcn | P 21/b 2/c 21/n | 26a | , | |||||
| 61 | Pbca | P 21/b 21/c 21/a | 29a | ||||||
| 62 | Pnma | P 21/n 21/m 21/a | 28a | , | |||||
| 63 | Cmcm | C 2/m 2/c 21/m | 18a | , | |||||
| 64 | Cmce | C 2/m 2/c 21/a | 19a | , | |||||
| 65 | Cmmm | C 2/m 2/m 2/m | 19s | ||||||
| 66 | Cccm | C 2/c 2/c 2/m | 20h | ||||||
| 67 | Cmme | C 2/m 2/m 2/e | 21h | ||||||
| 68 | Ccce | C 2/c 2/c 2/e | 22h | ||||||
| 69 | Fmmm | F 2/m 2/m 2/m | 21s | ||||||
| 70 | Fddd | F 2/d 2/d 2/d | 24h | ||||||
| 71 | Immm | I 2/m 2/m 2/m | 20s | ||||||
| 72 | Ibam | I 2/b 2/a 2/m | 23h | ||||||
| 73 | Ibca | I 2/b 2/c 2/a | 21a | ||||||
| 74 | Imma | I 2/m 2/m 2/a | 20a |
List of tetragonal
| Simple (P) | Body (I) |
|---|---|
 |
 |
| Number | Point group | Orbifold | Short name | Full name | Schoenflies | Fedorov | Shubnikov | Fibrifold |
|---|---|---|---|---|---|---|---|---|
| 75 | 4 | P4 | P 4 | 22s | ||||
| 76 | P41 | P 41 | 30a | |||||
| 77 | P42 | P 42 | 33a | |||||
| 78 | P43 | P 43 | 31a | |||||
| 79 | I4 | I 4 | 23s | |||||
| 80 | I41 | I 41 | 32a | |||||
| 81 | 4 | P4 | P 4 | 26s | ||||
| 82 | I4 | I 4 | 27s | |||||
| 83 | 4/m | P4/m | P 4/m | 28s | ||||
| 84 | P42/m | P 42/m | 41a | |||||
| 85 | P4/n | P 4/n | 29h | |||||
| 86 | P42/n | P 42/n | 42a | |||||
| 87 | I4/m | I 4/m | 29s | |||||
| 88 | I41/a | I 41/a | 40a | |||||
| 89 | 422 | P422 | P 4 2 2 | 30s | ||||
| 90 | P4212 | P4212 | 43a | | ||||
| 91 | P4122 | P 41 2 2 | 44a | |||||
| 92 | P41212 | P 41 21 2 | 48a | | ||||
| 93 | P4222 | P 42 2 2 | 47a | |||||
| 94 | P42212 | P 42 21 2 | 50a | | ||||
| 95 | P4322 | P 43 2 2 | 45a | |||||
| 96 | P43212 | P 43 21 2 | 49a | | ||||
| 97 | I422 | I 4 2 2 | 31s | |||||
| 98 | I4122 | I 41 2 2 | 46a | |||||
| 99 | 4mm | P4mm | P 4 m m | 24s | ||||
| 100 | P4bm | P 4 b m | 26h | |||||
| 101 | P42cm | P 42 c m | 37a | |||||
| 102 | P42nm | P 42 n m | 38a | |||||
| 103 | P4cc | P 4 c c | 25h | |||||
| 104 | P4nc | P 4 n c | 27h | |||||
| 105 | P42mc | P 42 m c | 36a | |||||
| 106 | P42bc | P 42 b c | 39a | |||||
| 107 | I4mm | I 4 m m | 25s | |||||
| 108 | I4cm | I 4 c m | 28h | |||||
| 109 | I41md | I 41 m d | 34a | |||||
| 110 | I41cd | I 41 c d | 35a | |||||
| 111 | 42m | P42m | P 4 2 m | 32s | ||||
| 112 | P42c | P 4 2 c | 30h | | ||||
| 113 | P421m | P 4 21 m | 52a | |||||
| 114 | P421c | P 4 21 c | 53a | |||||
| 115 | P4m2 | P 4 m 2 | 33s | |||||
| 116 | P4c2 | P 4 c 2 | 31h | |||||
| 117 | P4b2 | P 4 b 2 | 32h | |||||
| 118 | P4n2 | P 4 n 2 | 33h | |||||
| 119 | I4m2 | I 4 m 2 | 35s | |||||
| 120 | I4c2 | I 4 c 2 | 34h | |||||
| 121 | I42m | I 4 2 m | 34s | |||||
| 122 | I42d | I 4 2 d | 51a | |||||
| 123 | 4/m 2/m 2/m | P4/mmm | P 4/m 2/m 2/m | 36s | ||||
| 124 | P4/mcc | P 4/m 2/c 2/c | 35h | |||||
| 125 | P4/nbm | P 4/n 2/b 2/m | 36h | |||||
| 126 | P4/nnc | P 4/n 2/n 2/c | 37h | |||||
| 127 | P4/mbm | P 4/m 21/b 2/m | 54a | |||||
| 128 | P4/mnc | P 4/m 21/n 2/c | 56a | |||||
| 129 | P4/nmm | P 4/n 21/m 2/m | 55a | |||||
| 130 | P4/ncc | P 4/n 21/c 2/c | 57a | |||||
| 131 | P42/mmc | P 42/m 2/m 2/c | 60a | |||||
| 132 | P42/mcm | P 42/m 2/c 2/m | 61a | |||||
| 133 | P42/nbc | P 42/n 2/b 2/c | 63a | |||||
| 134 | P42/nnm | P 42/n 2/n 2/m | 62a | |||||
| 135 | P42/mbc | P 42/m 21/b 2/c | 66a | |||||
| 136 | P42/mnm | P 42/m 21/n 2/m | 65a | |||||
| 137 | P42/nmc | P 42/n 21/m 2/c | 67a | |||||
| 138 | P42/ncm | P 42/n 21/c 2/m | 65a | |||||
| 139 | I4/mmm | I 4/m 2/m 2/m | 37s | |||||
| 140 | I4/mcm | I 4/m 2/c 2/m | 38h | |||||
| 141 | I41/amd | I 41/a 2/m 2/d | 59a | |||||
| 142 | I41/acd | I 41/a 2/c 2/d | 58a |
List of trigonal
| Rhombohedral (R) | Hexagonal (P) |
|---|---|
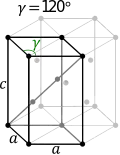 |
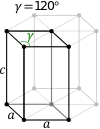 |
| Number | Point group | Orbifold | Short name | Full name | Schoenflies | Fedorov | Shubnikov | Fibrifold |
|---|---|---|---|---|---|---|---|---|
| 143 | 3 | P3 | P 3 | 38s | ||||
| 144 | P31 | P 31 | 68a | |||||
| 145 | P32 | P 32 | 69a | |||||
| 146 | R3 | R 3 | 39s | |||||
| 147 | 3 | P3 | P 3 | 51s | ||||
| 148 | R3 | R 3 | 52s | |||||
| 149 | 32 | P312 | P 3 1 2 | 45s | ||||
| 150 | P321 | P 3 2 1 | 44s | |||||
| 151 | P3112 | P 31 1 2 | 72a | |||||
| 152 | P3121 | P 31 2 1 | 70a | |||||
| 153 | P3212 | P 32 1 2 | 73a | |||||
| 154 | P3221 | P 32 2 1 | 71a | |||||
| 155 | R32 | R 3 2 | 46s | |||||
| 156 | 3m | P3m1 | P 3 m 1 | 40s | ||||
| 157 | P31m | P 3 1 m | 41s | |||||
| 158 | P3c1 | P 3 c 1 | 39h | |||||
| 159 | P31c | P 3 1 c | 40h | |||||
| 160 | R3m | R 3 m | 42s | |||||
| 161 | R3c | R 3 c | 41h | |||||
| 162 | 3 2/m | P31m | P 3 1 2/m | 56s | ||||
| 163 | P31c | P 3 1 2/c | 46h | |||||
| 164 | P3m1 | P 3 2/m 1 | 55s | |||||
| 165 | P3c1 | P 3 2/c 1 | 45h | |||||
| 166 | R3m | R 3 2/m | 57s | |||||
| 167 | R3c | R 3 2/c | 47h |
List of hexagonal
 |
| Number | Point group | Orbifold | Short name | Full name | Schoenflies | Fedorov | Shubnikov | Fibrifold |
|---|---|---|---|---|---|---|---|---|
| 168 | 6 | P6 | P 6 | 49s | ||||
| 169 | P61 | P 61 | 74a | |||||
| 170 | P65 | P 65 | 75a | |||||
| 171 | P62 | P 62 | 76a | |||||
| 172 | P64 | P 64 | 77a | |||||
| 173 | P63 | P 63 | 78a | |||||
| 174 | 6 | P6 | P 6 | 43s | ||||
| 175 | 6/m | P6/m | P 6/m | 53s | ||||
| 176 | P63/m | P 63/m | 81a | |||||
| 177 | 622 | P622 | P 6 2 2 | 54s | ||||
| 178 | P6122 | P 61 2 2 | 82a | |||||
| 179 | P6522 | P 65 2 2 | 83a | |||||
| 180 | P6222 | P 62 2 2 | 84a | |||||
| 181 | P6422 | P 64 2 2 | 85a | |||||
| 182 | P6322 | P 63 2 2 | 86a | |||||
| 183 | 6mm | P6mm | P 6 m m | 50s | ||||
| 184 | P6cc | P 6 c c | 44h | |||||
| 185 | P63cm | P 63 c m | 80a | |||||
| 186 | P63mc | P 63 m c | 79a | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/en.wikipedia.org/v1/":): {\displaystyle (*{:}6{\cdot}3{\cdot}2)} | ||||
| 187 | 6m2 | P6m2 | P 6 m 2 | 48s | ||||
| 188 | P6c2 | P 6 c 2 | 43h | |||||
| 189 | P62m | P 6 2 m | 47s | |||||
| 190 | P62c | P 6 2 c | 42h | |||||
| 191 | 6/m 2/m 2/m | P6/mmm | P 6/m 2/m 2/m | 58s | ||||
| 192 | P6/mcc | P 6/m 2/c 2/c | 48h | |||||
| 193 | P63/mcm | P 63/m 2/c 2/m | 87a | |||||
| 194 | P63/mmc | P 63/m 2/m 2/c | 88a |
List of cubic
| Simple (P) | Body centered (I) | Face centered (F) |
|---|---|---|
 |
 |
 |
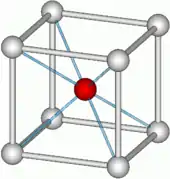 (221) Caesium chloride. Different colors for the two atom types.
(221) Caesium chloride. Different colors for the two atom types. (216) Sphalerite
(216) Sphalerite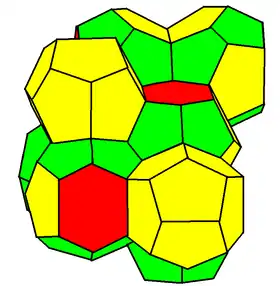 (223) Weaire–Phelan structure
(223) Weaire–Phelan structure
| Number | Point group | Orbifold | Short name | Full name | Schoenflies | Fedorov | Shubnikov | Conway | Fibrifold (preserving ) | Fibrifold (preserving , , ) |
|---|---|---|---|---|---|---|---|---|---|---|
| 195 | 23 | P23 | P 2 3 | 59s | ||||||
| 196 | F23 | F 2 3 | 61s | |||||||
| 197 | I23 | I 2 3 | 60s | |||||||
| 198 | P213 | P 21 3 | 89a | |||||||
| 199 | I213 | I 21 3 | 90a | |||||||
| 200 | 2/m 3 | Pm3 | P 2/m 3 | 62s | ||||||
| 201 | Pn3 | P 2/n 3 | 49h | |||||||
| 202 | Fm3 | F 2/m 3 | 64s | |||||||
| 203 | Fd3 | F 2/d 3 | 50h | |||||||
| 204 | Im3 | I 2/m 3 | 63s | |||||||
| 205 | Pa3 | P 21/a 3 | 91a | |||||||
| 206 | Ia3 | I 21/a 3 | 92a | |||||||
| 207 | 432 | P432 | P 4 3 2 | 68s | ||||||
| 208 | P4232 | P 42 3 2 | 98a | |||||||
| 209 | F432 | F 4 3 2 | 70s | |||||||
| 210 | F4132 | F 41 3 2 | 97a | |||||||
| 211 | I432 | I 4 3 2 | 69s | |||||||
| 212 | P4332 | P 43 3 2 | 94a | |||||||
| 213 | P4132 | P 41 3 2 | 95a | |||||||
| 214 | I4132 | I 41 3 2 | 96a | |||||||
| 215 | 43m | P43m | P 4 3 m | 65s | ||||||
| 216 | F43m | F 4 3 m | 67s | |||||||
| 217 | I43m | I 4 3 m | 66s | |||||||
| 218 | P43n | P 4 3 n | 51h | |||||||
| 219 | F43c | F 4 3 c | 52h | |||||||
| 220 | I43d | I 4 3 d | 93a | |||||||
| 221 | 4/m 3 2/m | Pm3m | P 4/m 3 2/m | 71s | ||||||
| 222 | Pn3n | P 4/n 3 2/n | 53h | |||||||
| 223 | Pm3n | P 42/m 3 2/n | 102a | |||||||
| 224 | Pn3m | P 42/n 3 2/m | 103a | |||||||
| 225 | Fm3m | F 4/m 3 2/m | 73s | |||||||
| 226 | Fm3c | F 4/m 3 2/c | 54h | |||||||
| 227 | Fd3m | F 41/d 3 2/m | 100a | |||||||
| 228 | Fd3c | F 41/d 3 2/c | 101a | |||||||
| 229 | Im3m | I 4/m 3 2/m | 72s | |||||||
| 230 | Ia3d | I 41/a 3 2/d | 99a |