Turn (biochemistry)

A turn is an element of secondary structure in proteins where the polypeptide chain reverses its overall direction.

For beta turns, see Beta turn.

Definition

According to one definition, a turn is a structural motif where the Cα atoms of two residues separated by a few (usually 1 to 5) peptide bonds are close (less than 7 Å [0.70 nm]).[1] The proximity of the terminal Cα atoms often correlates with formation of an inter main chain hydrogen bond between the corresponding residues. Such hydrogen bonding is the basis for the original, perhaps better known, turn definition. In many cases, but not all, the hydrogen-bonding and Cα-distance definitions are equivalent.

Types of turns
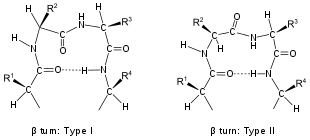
Scheme of beta turns (type I and type II)

Turns are classified[2] according to the separation between the two end residues:

  • In an α-turn the end residues are separated by four peptide bonds (i → i ± 4).
  • In a β-turn (the most common form), by three bonds (i → i ± 3).
  • In a γ-turn, by two bonds (i → i ± 2).
  • In a δ-turn, by one bond (i → i ± 1), which is sterically unlikely.
  • In a π-turn, by five bonds (i → i ± 5).
Ideal angles for different β-turn types.[3] Types VIa1, VIa2 and VIb turns are subject to the additional condition that residue i + 2(*) must be a cis-proline.
Typeφi + 1ψi + 1φi + 2ψi + 2
I −60°−30°−90°0°
II −60°120°80°0°
VIII −60°−30°−120°120°
I′ 60°30°90°0°
II′ 60°−120°−80°0°
VIa1 −60°120°−90°0°*
VIa2 −120°120°−60°0°*
VIb −135°135°−75°160°*
IV

turns excluded from all the above categories

Turns are classified by their backbone dihedral angles (see Ramachandran plot). A turn can be converted into its inverse turn (in which the main chain atoms have opposite chirality) by changing the sign on its dihedral angles. (The inverse turn is not a true enantiomer since the Cα atom chirality is maintained.) Thus, the γ-turn has two forms, a classical form with (φ, ψ) dihedral angles of roughly (75°, −65°) and an inverse form with dihedral angles (−75°, 65°). At least eight forms of the beta turn occur, varying in whether a cis isomer of a peptide bond is involved and on the dihedral angles of the central two residues. The classical and inverse β-turns are distinguished with a prime, e.g., type I and type I′ beta turns. If an i → i + 3 hydrogen bond is taken as the criterion for turns, the four categories of Venkatachalam[4] (I, II, II′, I′) suffice[5] to describe all possible beta turns. All four occur frequently in proteins but I is most common, followed by II, I′ and II′ in that order.

Loops

An ω-loop is a catch-all term for a longer, extended or irregular loop without fixed internal hydrogen bonding.

Multiple turns

In many cases, one or more residues are involved in two partially overlapping turns. For example, in a sequence of 5 residues, both residues 1 to 4 and residues 2 to 5 form a turn; in such a case, one speaks of an (i, i + 1) double turn. Multiple turns (up to sevenfold) occur commonly in proteins.[6] Beta bend ribbons are a different type of multiple turn.

Hairpins

A hairpin is a special case of a turn, in which the direction of the protein backbone reverses and the flanking secondary structure elements interact. For example, a beta hairpin connects two hydrogen-bonded, antiparallel β-strands (a rather confusing name, since a β-hairpin may contain many types of turns – α, β, γ, etc.).

Beta hairpins may be classified according to the number of residues that make up the turn - that is, that are not part of the flanking β-strands.[7] If this number is X or Y (according to two different definitions of β sheets) the β hairpin is defined as X:Y.

Beta turns at the loop ends of beta hairpins have a different distribution of types from the others; type I′ is commonest, followed by types II′, I and II.

Flexible linkers

Turns are sometimes found within flexible linkers or loops connecting protein domains. Linker sequences vary in length and are typically rich in polar uncharged amino acids. Flexible linkers allow connecting domains to freely twist and rotate to recruit their binding partners via protein domain dynamics. They also allow their binding partners to induce larger scale conformational changes by long-range allostery.[8][9][10]

Role in protein folding

Two hypotheses have been proposed for the role of turns in protein folding. In one view, turns play a critical role in folding by bringing together and enabling or allowing interactions between regular secondary structure elements. This view is supported by mutagenesis studies indicating a critical role for particular residues in the turns of some proteins. Also, nonnative isomers of X−Pro peptide bonds in turns can completely block the conformational folding of some proteins. In the opposing view, turns play a passive role in folding. This view is supported by the poor amino-acid conservation observed in most turns. The non-native isomers of many X−Pro peptide bonds in turns also have little or no effect on folding.

Beta turn prediction methods

Over the years, many beta turn prediction methods have been developed. Recently, Dr. Raghava's Group developed BetaTPred3 method which predicts a complete beta turn rather than individual residues falling into a beta turn. The method also achieves good accuracy and is the first method which predicts all 9 types of beta turns. Apart from prediction, this method can also be used to find the minimum number of mutations required to initiate or break a beta turn in a protein at a desired location.

See also

References
  1. see Rose et al. 1985 in the References
  2. Toniolo 1980
  3. Venkatachalam 1968; Richardson 1981; Hutchinson and Thornton 1994
  4. Venkatachalam, CM (1968). "Stereochemical criteria for polypeptides and proteins. V. Conformations of a system of three linked peptide units" (PDF). Biopolymers. 6 (10): 1425–1436. doi:10.1002/bip.1968.360061006. hdl:2027.42/37819. PMID 5685102.
  5. Richardson, JS (1981). "The anatomy and taxonomy of protein structure". Advances in Protein Chemistry Volume 34. pp. 167–339. doi:10.1016/s0065-3233(08)60520-3. ISBN 9780120342341. PMID 7020376. {{cite book}}: |journal= ignored (help)
  6. Hutchinson 1994, p 2213
  7. Sibanda 1989
  8. Dunker AK, Lawson JD, Brown CJ, Williams RM, Romero P, Oh JS, Oldfield CJ, Campen AM, Ratliff CM, Hipps KW, Ausio J, Nissen MS, Reeves R, Kang C, Kissinger CR, Bailey RW, Griswold MD, Chiu W, Garner EC, Obradovic Z (2001). "Intrinsically disordered protein". Journal of Molecular Graphics & Modelling. 19 (1): 26–59. CiteSeerX 10.1.1.113.556. doi:10.1016/s1093-3263(00)00138-8. PMID 11381529.
  9. Bu Z, Callaway DJ (2011). "Proteins move! Protein dynamics and long-range allostery in cell signaling". Protein Structure and Diseases. Advances in Protein Chemistry and Structural Biology. Vol. 83. pp. 163–221. doi:10.1016/B978-0-12-381262-9.00005-7. ISBN 9780123812629. PMID 21570668.
  10. Compiani M, Capriotti E (Dec 2013). "Computational and theoretical methods for protein folding" (PDF). Biochemistry. 52 (48): 8601–24. doi:10.1021/bi4001529. PMID 24187909. Archived from the original (PDF) on 2015-09-04.

Literature

These references are ordered by date.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.