Lorentz oscillator model

The model is derived by modeling an electron orbiting a massive, stationary nucleus as a spring-mass-damper system.[2][3][4] The electron is modeled to be connected to the nucleus via a hypothetical spring and its motion is damped by via a hypothetical damper. The damping force ensures that the oscillator's response is finite at its resonance frequency. For a time-harmonic driving force which originates from the electric field, Newton’s second law can be applied to the electron to obtain the motion of the electron and expressions for the dipole moment, polarization, susceptibility, and dielectric function.[4]

Equation of motion for electron oscillator:

$${\displaystyle {\begin{aligned}\mathbf {F} _{\text{net}}=\mathbf {F} _{\text{damping}}+\mathbf {F} _{\text{spring}}+\mathbf {F} _{\text{driving}}&=m{\frac {\mathrm {d} ^{2}\mathbf {r} }{\mathrm {d} t^{2}}}\\[1ex]{\frac {-m}{\tau }}{\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}-k\mathbf {r} -{e}\mathbf {E} (t)&=m{\frac {\mathrm {d} ^{2}\mathbf {r} }{\mathrm {d} t^{2}}}\\[1ex]{\frac {\mathrm {d} ^{2}\mathbf {r} }{\mathrm {d} t^{2}}}+{\frac {1}{\tau }}{\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}+\omega _{0}^{2}\mathbf {r} \;&=\;{\frac {-e}{m}}\mathbf {E} (t)\end{aligned}}}$$

where

• ${\displaystyle \mathbf {r} }$ is the displacement of charge from the rest position,
• ${\displaystyle t}$ is time,
• ${\displaystyle \tau }$ is the relaxation time/scattering time,
• ${\displaystyle k}$ is a constant factor characteristic of the spring,
• ${\displaystyle m}$ is the effective mass of the electron,
• ${\textstyle \omega _{0}={\sqrt {k/m}}}$ is the resonance frequency of the oscillator,
• ${\displaystyle e}$ is the elementary charge,
• ${\displaystyle \mathbf {E} (t)}$ is the electric field.

For time-harmonic fields:

$${\displaystyle \mathbf {E} (t)=\mathbf {E} _{0}e^{-i\omega t}}$$

$${\displaystyle \mathbf {r} (t)=\mathbf {r} _{0}e^{-i\omega t}}$$

The stationary solution of this equation of motion is:

$${\displaystyle \mathbf {r} (\omega )={\frac {\frac {-e}{m}}{\omega _{0}^{2}-\omega ^{2}-i\omega /\tau }}\mathbf {E} (\omega )}$$

The fact that the above solution is complex means there is a time delay (phase shift) between the driving electric field and the response of the electron’s motion.[4]

The displacement, ${\displaystyle \mathbf {r} }$, induces a dipole moment, ${\displaystyle \mathbf {p} }$, given by

$${\displaystyle \mathbf {p} (\omega )=-e\mathbf {r} (\omega )={\hat {\alpha }}(\omega )\mathbf {E} (\omega ).}$$

${\displaystyle {\hat {\alpha }}(\omega )}$ is the polarizability of single oscillator, given by

$${\displaystyle {\hat {\alpha }}(\omega )={\frac {e^{2}}{m}}{\frac {1}{(\omega _{0}^{2}-\omega ^{2})-i\omega /\tau }}.}$$

The polarization ${\displaystyle \mathbf {P} }$ is the dipole moment per unit volume. For macroscopic material properties N is the density of charges (electrons) per unit volume. Considering that each electron is acting with the same dipole moment we have the polarization as below

$${\displaystyle \mathbf {P} =N\mathbf {p} =N{\hat {\alpha }}(\omega )\mathbf {E} (\omega ).}$$

The electric displacement ${\displaystyle \mathbf {D} }$ is related to the polarization density ${\displaystyle \mathbf {P} }$ by

$${\displaystyle \mathbf {D} ={\hat {\varepsilon }}\mathbf {E} =\mathbf {E} +4\pi \mathbf {P} =(1+4\pi N{\hat {\alpha }})\mathbf {E} }$$

Lorentz oscillator model. The real (blue solid line) and imaginary (orange dashed line) components of relative permittivity are plotted for a single oscillator model with parameters ${\displaystyle \omega _{0}=\mathrm {23.8\,THz} }$ (12.6 μm), ${\displaystyle s/\omega _{0}^{2}=\mathrm {3.305} }$, ${\displaystyle \Gamma /\omega _{0}=\mathrm {0.006} }$, and ${\displaystyle \varepsilon _{\infty }=\mathrm {6.7} }$. These parameters approximate hexagonal silicon carbide.[5]

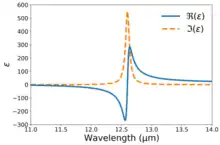
The complex dielectric function is given by

$${\displaystyle {\hat {\varepsilon }}(\omega )=1+{\frac {4\pi Ne^{2}}{m}}{\frac {1}{(\omega _{0}^{2}-\omega ^{2})-i\omega /\tau }}}$$

where ${\displaystyle 4\pi Ne^{2}/m=\omega _{p}^{2}}$ and ${\displaystyle \omega _{p}}$ is the so called plasma frequency.

In practice, the model is commonly modified to account for multiple absorption mechanisms present in a medium. The modified version is given by[6]

$${\displaystyle {\hat {\varepsilon }}(\omega )=\varepsilon _{\infty }+\sum _{j}\chi _{j}^{L}(\omega$$ ;\omega _{0,j})}

where

$${\displaystyle \chi _{j}^{L}(\omega$$ ;\omega _{0,j})={\frac {s_{j}}{\omega _{0,j}^{2}-\omega ^{2}-i\Gamma _{j}\omega }}}

and

• ${\displaystyle \varepsilon _{\infty }}$ is the value of the dielectric function at infinite frequency, which can be used as an adjustable parameter to account for high frequency absorption mechanisms,
• ${\displaystyle s_{j}=\omega _{p}^{2}f_{j}}$ and ${\displaystyle f_{j}}$ is related to the strength of the ${\displaystyle j}$th absorption mechanism,
• ${\displaystyle \Gamma _{j}=1/\tau }$.

Separating the real and imaginary components,

$${\displaystyle {\hat {\varepsilon }}(\omega )=\varepsilon _{1}(\omega )+i\varepsilon _{2}(\omega )=\left[\varepsilon _{\infty }+\sum _{j}{\frac {s_{j}(\omega _{0,j}^{2}-\omega ^{2})}{\left(\omega _{0,j}^{2}-\omega ^{2}\right)^{2}+\left(\Gamma _{j}\omega \right)^{2}}}\right]+i\left[\sum _{j}{\frac {s_{j}(\Gamma _{j}\omega )}{\left(\omega _{0,j}^{2}-\omega ^{2}\right)^{2}+\left(\Gamma _{j}\omega \right)^{2}}}\right]}$$

The complex optical conductivity in general is related to the complex dielectric function

$${\displaystyle {\hat {\sigma }}(\omega )={\frac {\omega }{4\pi i}}\left({\hat {\varepsilon }}(\omega )-1\right)}$$

Substituting the formula of ${\displaystyle {\hat {\varepsilon }}(\omega )}$ in the equation above we obtain

$${\displaystyle {\hat {\sigma }}(\omega )={\frac {Ne^{2}}{m}}{\frac {\omega }{\omega /\tau +i\left(\omega _{0}^{2}-\omega ^{2}\right)}}}$$

Separating the real and imaginary components,

$${\displaystyle {\hat {\sigma }}(\omega )=\sigma _{1}(\omega )+i\sigma _{2}(\omega )={\frac {Ne^{2}}{m}}{\frac {\frac {\omega ^{2}}{\tau }}{\left(\omega _{0}^{2}-\omega ^{2}\right)^{2}+\omega ^{2}/\tau ^{2}}}-i{\frac {Ne^{2}}{m}}{\frac {\left(\omega _{0}^{2}-\omega ^{2}\right)\omega }{\left(\omega _{0}^{2}-\omega ^{2}\right)^{2}+\omega ^{2}/\tau ^{2}}}}$$

• Cauchy equation
• Sellmeier equation
• Forouhi–Bloomer model
• Tauc–Lorentz model
• Brendel–Bormann oscillator model