Magnetic helicity

Generally, the helicity ${\displaystyle H^{\mathbf {f} }}$ of a smooth vector field ${\displaystyle \mathbf {f} }$ confined to a volume ${\displaystyle V}$ is the standard measure of the extent to which the field lines wrap and coil around one another.[14][2] It is defined as the volume integral over ${\displaystyle V}$ of the scalar product of ${\displaystyle \mathbf {f} }$ and its curl, ${\displaystyle \nabla \times {\mathbf {f} }}$:

${\displaystyle H^{\mathbf {f} }=\int _{V}{\mathbf {f} }\cdot \left(\nabla \times {\mathbf {f} }\right)\ dV.}$

The name "helicity" relies on the fact that the trajectory of a fluid particle in a fluid with velocity ${\displaystyle {\boldsymbol {v}}}$ and vorticity ${\displaystyle {\boldsymbol {\omega }}=\nabla \times {\boldsymbol {v}}}$ forms a helix in regions where the kinetic helicity ${\displaystyle \textstyle H^{K}=\int \mathbf {v} \cdot {\boldsymbol {\omega }}\neq 0}$. When ${\displaystyle \textstyle H^{K}>0}$, the helix is right-handed and when ${\displaystyle \textstyle H^{K}<0}$ it is left-handed. This behavior is very similar to magnetic field lines.

Regions, where magnetic helicity is not zero, can also contain other sorts of magnetic structures as helical magnetic field lines. Magnetic helicity is indeed a generalization of the topological concept of linking number to the differential quantities required to describe the magnetic field.[6] The linking number describes how many magnetic field lines are interlinked (see [9] for a mathematical proof of it). Through a simple experiment with paper and scissors, one can show that magnetic field lines which turn around each other can be considered as being interlinked (figure 5 in [9]). Thus, the presence of magnetic helicity can be interpreted as helical magnetic field lines, interlinked magnetic structures, but also magnetic field lines turning around each other.

Example of helical structures in the DNA. It looks similar for helical magnetic field lines. Topologically speaking: units of writhe and units of twist can be interchanged.

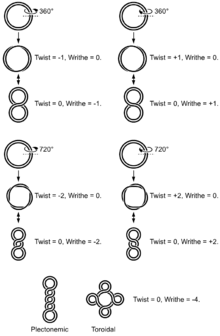
Magnetic field lines turning around each other can take several shapes. Let's consider for example a set of turning magnetic field lines in a close neighborhood, which forms a so-called "magnetic flux tube" (see figure for an illustration).

"Twist" means that the flux tube rotates around its own axis (figures with Twist=${\displaystyle \pm 1}$). Topologically speaking, units of twist and of writhe (which means, the rotation of the flux tube axis itself — figures with Writhe=${\displaystyle \pm 1}$) can be transformed into each other. One can also show that knots are also equivalent to units of twist and/or writhe.[2]

As with many quantities in electromagnetism, magnetic helicity (which describes magnetic field lines) is closely related to fluid mechanical helicity (which describes fluid flow lines) and their dynamics are interlinked.[5][18]

In the late 1950s, Lodewijk Woltjer and Walter M. Elsässer discovered independently the ideal invariance of magnetic helicity,[4][3] that is, its conservation when resistivity is zero. Woltjer's proof, valid for a closed system, is repeated in the following:

In ideal magnetohydrodynamics, the time evolution of a magnetic field and magnetic vector potential can be expressed using the induction equation as

${\displaystyle {\frac {\partial {\mathbf {B} }}{\partial t}}=\nabla \times ({\mathbf {v} }\times {\mathbf {B} }),\quad {\frac {\partial {\mathbf {A} }}{\partial t}}={\mathbf {v} }\times {\mathbf {B} }+\nabla \Phi ,}$

respectively, where ${\displaystyle \nabla \Phi }$ is a scalar potential given by the gauge condition (see § Gauge considerations). Choosing the gauge so that the scalar potential vanishes, ${\displaystyle \nabla \Phi =\mathbf {0} }$, the time evolution of magnetic helicity in a volume ${\displaystyle V}$ is given by:

${\displaystyle {\begin{aligned}{\frac {\partial H^{\mathbf {M} }}{\partial t}}&=\int _{V}\left({\frac {\partial {\mathbf {A} }}{\partial t}}\cdot {\mathbf {B} }+{\mathbf {A} }\cdot {\frac {\partial {\mathbf {B} }}{\partial t}}\right)dV\\&=\int _{V}({\mathbf {v} }\times {\mathbf {B} })\cdot {\mathbf {B} }\ dV+\int _{V}{\mathbf {A} }\cdot \left(\nabla \times {\frac {\partial {\mathbf {A} }}{\partial t}}\right)dV.\end{aligned}}}$

The dot product in the integrand of the first term is zero since ${\displaystyle {\mathbf {B} }}$ is orthogonal to the cross product ${\displaystyle {\mathbf {v} }\times {\mathbf {B} }}$, and the second term can be integrated by parts to give

${\displaystyle {\frac {\partial H^{\mathbf {M} }}{\partial t}}=\int _{V}\left(\nabla \times {\mathbf {A} }\right)\cdot {\frac {\partial {\mathbf {A} }}{\partial t}}\ dV+\int _{\partial V}\left({\mathbf {A} }\times {\frac {\partial {\mathbf {A} }}{\partial t}}\right)\cdot d\mathbf {S} }$

where the second term is a surface integral over the boundary surface ${\displaystyle \partial V}$ of the closed system. The dot product in the integrand of the first term is zero because ${\displaystyle \nabla \times {\mathbf {A} }={\mathbf {B} }}$ is orthogonal to ${\displaystyle \partial {\mathbf {A} }/\partial t.}$ The second term also vanishes because motions inside the closed system cannot affect the vector potential outside, so that at the boundary surface ${\displaystyle \partial {\mathbf {A} }/\partial t=\mathbf {0} }$ since the magnetic vector potential is a continuous function. Therefore,

${\displaystyle {\frac {\partial H^{\mathbf {M} }}{\partial t}}=0,}$

and magnetic helicity is ideally conserved. In all situations where magnetic helicity is gauge invariant, magnetic helicity is ideally conserved without the need for the specific gauge choice ${\displaystyle \nabla \Phi =\mathbf {0} .}$

Magnetic helicity remains conserved in a good approximation even with a small but finite resistivity, in which case magnetic reconnection dissipates energy.[6][9]

Small-scale helical structures tend to form larger and larger magnetic structures. This can be called an inverse transfer in Fourier space, as opposed to the (direct) energy cascade in three dimensional turbulent hydrodynamical flows. The possibility of such an inverse transfer has first been proposed by Uriel Frisch and collaborators[5] and has been verified through many numerical experiments.[19][20][21][22][23][24] As a consequence, the presence of magnetic helicity is a possibility to explain the existence and sustainment of large-scale magnetic structures in the Universe.

An argument for this inverse transfer taken from[5] is repeated here, which is based on the so-called "realizability condition" on the magnetic helicity Fourier spectrum ${\displaystyle {\hat {H}}_{\mathbf {k} }^{M}={\hat {\mathbf {A} }}_{\mathbf {k} }^{*}\cdot {\hat {\mathbf {B} }}_{\mathbf {k} }}$ (where ${\displaystyle {\hat {\mathbf {B} }}_{\mathbf {k} }}$ is the Fourier coefficient at the wavevector ${\displaystyle {\mathbf {k} }}$ of the magnetic field ${\displaystyle {\mathbf {B} }}$, and similarly for ${\displaystyle {\hat {\mathbf {A} }}}$, the star denoting the complex conjugate). The "realizability condition" corresponds to an application of Cauchy-Schwarz inequality, which yields:

$${\displaystyle \left|{\hat {H}}_{\mathbf {k} }^{M}\right|\leq {\frac {2E_{\mathbf {k} }^{M}}{|{\mathbf {k} }|}},}$$

with ${\textstyle E_{\mathbf {k} }^{M}={\frac {1}{2}}{\hat {\mathbf {B} }}_{\mathbf {k} }^{*}\cdot {\hat {\mathbf {B} }}_{\mathbf {k} }}$ the magnetic energy spectrum. To obtain this inequality, the fact that ${\displaystyle |{\hat {\mathbf {B} }}_{\mathbf {k} }|=|{\mathbf {k} }||{\hat {\mathbf {A} }}_{\mathbf {k} }^{\perp }|}$ (with ${\displaystyle {\hat {\mathbf {A} }}_{\mathbf {k} }^{\perp }}$ the solenoidal part of the Fourier transformed magnetic vector potential, orthogonal to the wavevector in Fourier space) has been used, since ${\displaystyle {\hat {\mathbf {B} }}_{\mathbf {k} }=i{\mathbf {k} }\times {\hat {\mathbf {A} }}_{\mathbf {k} }}$. The factor 2 is not present in the paper[5] since the magnetic helicity is defined there alternatively as ${\displaystyle {\frac {1}{2}}\int _{V}{\mathbf {A} }\cdot {\mathbf {B} }\ dV}$.

One can then imagine an initial situation with no velocity field and a magnetic field only present at two wavevectors ${\displaystyle \mathbf {p} }$ and ${\displaystyle \mathbf {q} }$. We assume a fully helical magnetic field, which means that it saturates the realizability condition: ${\displaystyle \left|{\hat {H}}_{\mathbf {p} }^{M}\right|={\frac {2E_{\mathbf {p} }^{M}}{|{\mathbf {p} }|}}}$ and ${\displaystyle \left|{\hat {H}}_{\mathbf {q} }^{M}\right|={\frac {2E_{\mathbf {q} }^{M}}{|{\mathbf {q} }|}}}$. Assuming that all the energy and magnetic helicity transfers are done to another wavevector ${\displaystyle \mathbf {k} }$, the conservation of magnetic helicity on the one hand and of the total energy ${\displaystyle E^{T}=E^{M}+E^{K}}$ (the sum of magnetic and kinetic energy) on the other hand gives:

$${\displaystyle H_{\mathbf {k} }^{M}=H_{\mathbf {p} }^{M}+H_{\mathbf {q} }^{M},}$$

$${\displaystyle E_{\mathbf {k} }^{T}=E_{\mathbf {p} }^{T}+E_{\mathbf {q} }^{T}=E_{\mathbf {p} }^{M}+E_{\mathbf {q} }^{M}.}$$

The second equality for energy comes from the fact that we consider an initial state with no kinetic energy. Then we have the necessarily ${\displaystyle |\mathbf {k} |\leq \max(|\mathbf {p} |,|\mathbf {q} |)}$. Indeed, if we would have ${\displaystyle |\mathbf {k} |>\max(|\mathbf {p} |,|\mathbf {q} |)}$, then:

$${\displaystyle H_{\mathbf {k} }^{M}=H_{\mathbf {p} }^{M}+H_{\mathbf {q} }^{M}={\frac {2E_{\mathbf {p} }^{M}}{|\mathbf {p} |}}+{\frac {2E_{\mathbf {q} }^{M}}{|\mathbf {q} |}}>{\frac {2\left(E_{\mathbf {p} }^{M}+E_{\mathbf {q} }^{M}\right)}{|\mathbf {k} |}}={\frac {2E_{\mathbf {k} }^{T}}{|\mathbf {k} |}}\geq {\frac {2E_{\mathbf {k} }^{M}}{|\mathbf {k} |}},}$$

which would break the realizability condition. This means that ${\displaystyle |\mathbf {k} |\leq \max(|\mathbf {p} |,|\mathbf {q} |)}$. In particular, for ${\displaystyle |{\mathbf {p} }|=|{\mathbf {q} }|}$, the magnetic helicity is transferred to a smaller wavevector, which means to larger scales.

Magnetic helicity is a gauge-dependent quantity, because ${\displaystyle \mathbf {A} }$ can be redefined by adding a gradient to it (gauge choosing). However, for perfectly conducting boundaries or periodic systems without a net magnetic flux, the magnetic helicity contained in the whole domain is gauge invariant,[17] that is, independent of the gauge choice. A gauge-invariant relative helicity has been defined for volumes with non-zero magnetic flux on their boundary surfaces.[6]

• Woltjer's theorem

• A. A. Pevtsov's Helicity Page
• Mitch Berger's Publications Page