Matter power spectrum

Let ${\displaystyle \delta (\mathbf {x} )}$ represent the matter overdensity, a dimensionless quantity defined as:

$${\displaystyle \delta (\mathbf {x} )={\frac {\rho (\mathbf {x} )-{\bar {\rho }}}{\bar {\rho }}},}$$

where ${\displaystyle {\bar {\rho }}}$ is the average matter density over all space.

The power spectrum is most commonly understood as the Fourier transform of the autocorrelation function, ${\displaystyle \xi }$, mathematically defined as:

$${\displaystyle \xi (r)=\langle \delta (\mathbf {x} )\delta (\mathbf {x} ')\rangle ={\frac {1}{V}}\int d^{3}\mathbf {x} \,\delta (\mathbf {x} )\delta (\mathbf {x} -\mathbf {r} ),}$$

for ${\displaystyle \mathbf {r} =\mathbf {x} -\mathbf {x} '}$. This then determines the easily derived relationship to the power spectrum, ${\displaystyle P(\mathbf {k} )}$, that is ${\displaystyle \xi (r)=\int {\frac {d^{3}k}{(2\pi )^{3}}}P(k)e^{i\mathbf {k} \cdot (\mathbf {x} -\mathbf {x} ')}.}$

Equivalently, letting ${\displaystyle {\tilde {\delta }}(\mathbf {k} )}$ denote the Fourier transform of the overdensity ${\displaystyle \delta (\mathbf {x} )}$, the power spectrum is given by the following average over Fourier space:[1]

$${\displaystyle \langle {\tilde {\delta }}(\mathbf {k} ){\tilde {\delta }}^{*}(\mathbf {k} ')\rangle =(2\pi )^{3}P(k)\delta ^{3}(\mathbf {k} -\mathbf {k} ')}$$

(note that ${\displaystyle \delta ^{3}}$ is not an overdensity but the Dirac delta function).

Since ${\displaystyle P(k)}$ has dimensions of (length)³, the power spectrum is also sometimes given in terms of the dimensionless function:[1]

$${\displaystyle \Delta ^{2}(k)={\frac {k^{3}P(k)}{2\pi ^{2}}}.}$$

If the autocorrelation function describes the probability of a galaxy at a distance ${\displaystyle r}$ from another galaxy, the matter power spectrum decomposes this probability into characteristic lengths, ${\displaystyle k\approx 2\pi /L}$, and its amplitude describes the degree to which each characteristic length contributes to the total over-probability.

The overall shape of the matter power spectrum is best understood in terms of the linear perturbation theory analysis of the growth of structure, which predicts to first order that the power spectrum grows according to:

$${\displaystyle P(\mathbf {k} ,t)=D_{+}^{2}(t)P(\mathbf {k} ,t_{0})=D_{+}^{2}(t)P_{0}(\mathbf {k} )}$$

Where ${\displaystyle D_{+}(t)}$ is the linear growth factor in the density, that is to first order ${\displaystyle \delta (r,t)=D_{+}(t)\delta _{0}(r)}$, and ${\displaystyle P_{0}(\mathbf {k} )}$ is commonly referred to as the primordial matter power spectrum. Determining the primordial ${\displaystyle P_{0}(\mathbf {k} )}$ is a question that relates to the physics of inflation.

The simplest ${\displaystyle P_{0}(\mathbf {k} )}$ is the Harrison–Zel'dovich spectrum,[2][3] which characterizes ${\displaystyle P_{0}(\mathbf {k} )}$ according to a power law, ${\displaystyle P_{0}(\mathbf {k} )=Ak}$. More advanced primordial spectra include the use of a transfer function which mediates the transition from the universe being radiation dominated to being matter dominated.

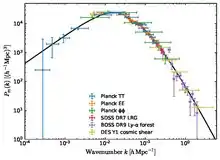
The broad shape of the matter power spectrum is determined by the growth of large-scale structure, with the turnover (the point where the spectrum goes from increasing with k to decreasing with k) at ${\displaystyle \mathbf {k} \approx 2\times 10^{-2}~h~{\text{Mpc}}^{-1}}$, corresponding to ${\displaystyle \lambda _{m}=350~h^{-1}~{\text{Mpc}}}$ (where h is the dimensionless Hubble constant).[4] The co-moving wavenumber corresponding to the maximum power in the mass power spectrum is determined by the size of the cosmic particle horizon at the time of matter-radiation equality, and therefore depends on the mean density of matter and to a lesser extent on the number of neutrino families (${\displaystyle N\geq 3}$), ${\displaystyle k_{\text{eq}}=(2\Omega _{M}H_{0}^{2}z_{\text{eq}}/c^{2})=7.3\times 10^{-2}\Omega _{M}h^{2}{\text{Mpc}}^{-1}}$, for ${\displaystyle T_{\text{cmb}}=2.728~\mathrm {K} }$. The ${\displaystyle P_{0}(k)}$ at smaller k (equivalently, larger scales) corresponds to scales which were larger than the particle horizon at the time of the transition from the regime of radiation dominance to that of matter dominance. [5][6]

• Dodelson, Scott (2003). Modern Cosmology. Academic Press. ISBN 978-0-12-219141-1.
• Theuns, Physical Cosmology
• Michael L. Norman, Simulating Galaxy Clusters