Maxwell's theorem (geometry)

Maxwell's theorem is the following statement about triangles in the plane.

For a given triangle ${\displaystyle ABC}$ and a point ${\displaystyle V}$ not on the sides of that triangle construct a second triangle ${\displaystyle A'B'C'}$, such that the side ${\displaystyle A'B'}$ is parallel to the line segment ${\displaystyle CV}$, the side ${\displaystyle A'C'}$ is parallel to the line segment ${\displaystyle BV}$ and the side ${\displaystyle B'C'}$ is parallel to the line segment ${\displaystyle AV}$. Then the parallel to ${\displaystyle AB}$ through ${\displaystyle C'}$, the parallel to ${\displaystyle BC}$ through ${\displaystyle A'}$ and the parallel to ${\displaystyle AC}$ through ${\displaystyle B'}$ intersect in a common point ${\displaystyle V'}$.

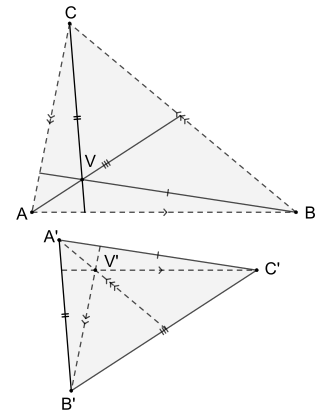
Line segments with identical markings are parallel.
If the sides of the triangle${\displaystyle A'B'C'}$ are parallel to the according cevians of triangle ${\displaystyle ABC}$, which are intersecting in a common point ${\displaystyle V'}$, then the cevians of triangle ${\displaystyle A'B'C'}$, which are parallel to the according sides of triangle ${\displaystyle ABC}$ intersect in a common point ${\displaystyle V'}$ as well

The theorem is named after the physicist James Clerk Maxwell (1831–1879), who proved it in his work on reciprocal figures, which are of importance in statics.