Metric lattice
In the mathematical study of order, a metric lattice L is a lattice that admits a positive valuation: a function v ∈ L → ℝ satisfying, for any a, b ∈ L,[1]

and
Relation to other notions
A Boolean algebra is a metric lattice; any finitely-additive measure on its Stone dual gives a valuation.[2]: 252–254
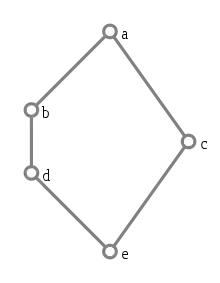
Every metric lattice is a modular lattice,[1] c.f. lower picture. It is also a metric space, with distance function given by[3]
With that metric, the join and meet are uniformly continuous contractions,[2]: 77 and so extend to the metric completion (metric space). That lattice is usually not the Dedekind-MacNeille completion, but it is conditionally complete.[2]: 80
Applications
In the study of fuzzy logic and interval arithmetic, the space of uniform distributions is a metric lattice.[3] Metric lattices are also key to von Neumann's construction of the continuous projective geometry.[2]: 126 A function satisfies the one-dimensional wave equation if and only if it is a valuation for the lattice of spacetime coordinates with the natural partial order. A similar result should apply to any partial differential equation solvable by the method of characteristics, but key features of the theory are lacking.[2]: 150–151
References
- Rutherford, Daniel Edwin (1965). Introduction to Lattice Theory. Oliver and Boyd. pp. 20–22.
- Birkhoff, Garrett (1948). Lattice Theory. AMS Colloquium Publications 25 (Revised ed.). New York City: AMS. hdl:2027/iau.31858027322886 – via HathiTrust.
- Kaburlasos, V. G. (2004). "FINs: Lattice Theoretic Tools for Improving Prediction of Sugar Production From Populations of Measurements." IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 34(2), 1017–1030. doi:10.1109/tsmcb.2003.818558