Mice problem
In mathematics, the mice problem is a continuous pursuit–evasion problem in which a number of mice (or insects, dogs, missiles, etc.) are considered to be placed at the corners of a regular polygon. In the classic setup, each then begins to move towards its immediate neighbour (clockwise or anticlockwise). The goal is often to find out at what time the mice meet.

The most common version has the mice starting at the corners of a unit square, moving at unit speed. In this case they meet after a time of one unit, because the distance between two neighboring mice always decreases at a speed of one unit. More generally, for a regular polygon of unit-length sides, the distance between neighboring mice decreases at a speed of , so they meet after a time of .[1][2]
Path of the mice
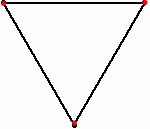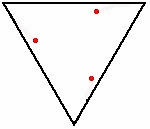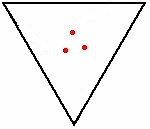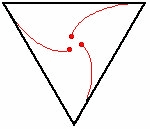
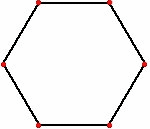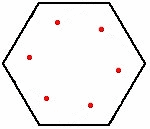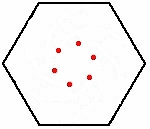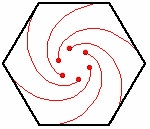
For all regular polygons, each mouse traces out a pursuit curve in the shape of a logarithmic spiral. These curves meet in the center of the polygon.[3]
In media
In Dara Ó Briain: School of Hard Sums, the mice problem is discussed. Instead of 4 mice, 4 ballroom dancers are used.[4]
References
- Gamow, George; Stern, Marvin (1958). Puzzle Math. Viking Press. pp. 112–114.
- Lucas, Édouard (1877). "Problem of the Three Dogs". Nouv. Corresp. Math. 3: 175–176.
- Bernhart, Arthur (1959). "Polygons of pursuit". Scripta Mathematica. 24: 23–50. MR 0104178.
- Ó Briain, Dara; du Sautoy, Marcus; Watson, Mark; Brigstocke, Marcus (March 2014). "Downton Abacus: The Maths of Wealth". Dara Ó Briain: School of Hard Sums. Season 3. Episode 4. 24 minutes in. Dave.
External links
- Weisstein, Eric W. "Mice Problem". MathWorld.
- Zeno's Mice (Ants) Problem and the Logarithmic Spirals - YouTube lecture with equation derivation