Midpoint theorem (conics)
In geometry, the midpoint theorem describes a property of parallel chords in a conic. It states that the midpoints of parallel chords in a conic are located on a common line.
The common line (segment) for the midpoints is also called the diameter of a conic. For a circle, ellipse or hyperbola the diameter goes through its center. For a parabola the diameter is always perpendicular to its directrix and for a pair of intersecting lines the diameter goes through the point of intersection.
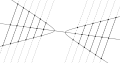hyperbola
circle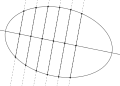
ellipse
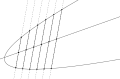parabola
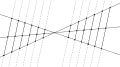intersecting lines
References
- David A. Brannan, David Alexander Brannan, Matthew F. Esplen, Jeremy J. Gray (1999) Geometry Cambridge University Press ISBN 9780521597876, pages 59–66
- Aleksander Simonic (November 2012) "On a Problem Concerning Two Conics". In: Crux Mathematicorum, volume 38(9) pages 372–377
- C. G. Gibson (2003) Elementary Euclidean Geometry: An Introduction. Cambridge University Press ISBN 9780521834483 pages 65–68
External links
- Locus of Midpoints of Parallel Chords of Central Conic passes through Center at the Proof Wiki
- midpoints of parallel chords in conics lie on a common line - interactive illustration
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.