Morley centers

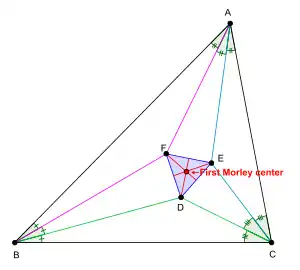
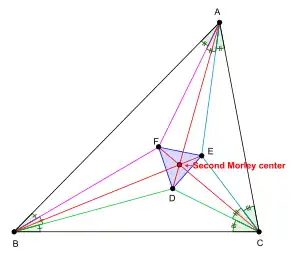
In plane geometry, the Morley centers are two special points associated with a triangle. Both of them are triangle centers. One of them called first Morley center[1] (or simply, the Morley center[2] ) is designated as X(356) in Clark Kimberling's Encyclopedia of Triangle Centers, while the other point called second Morley center[1] (or the 1st Morley–Taylor–Marr Center[2]) is designated as X(357). The two points are also related to Morley's trisector theorem which was discovered by Frank Morley in around 1899.

Definitions

Let △DEF be the triangle formed by the intersections of the adjacent angle trisectors of triangle △ABC. △DEF is called the Morley triangle of △ABC. Morley's trisector theorem states that the Morley triangle of any triangle is always an equilateral triangle.

First Morley center


Let △DEF be the Morley triangle of △ABC. The centroid of △DEF is called the first Morley center of △ABC.[1][3]

Second Morley center

Let △DEF be the Morley triangle of △ABC. Then, the lines AD, BE, CF are concurrent. The point of concurrence is called the second Morley center of triangle △ABC.[1][3]

Trilinear coordinates

First Morley center

The trilinear coordinates of the first Morley center of triangle △ABC are [1]

Second Morley center

The trilinear coordinates of the second Morley center are

References
  1. Kimberling, Clark. "1st and 2nd Morley centers". Retrieved 16 June 2012.
  2. Kimberling, Clark. "X(356) = Morley center". Encyclopedia of Triangle Centers. Retrieved 16 June 2012.
  3. Weisstein, Eric W. "Morley Centers". Mathworld – A Wolfram Web Resource. Retrieved 16 June 2012.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.