Morse–Smale system

Consider a smooth and complete vector field X defined on a compact differentiable manifold M with dimension n. The flow defined by this vector field is a Morse-Smale system if

1. X has only a finite number of singular points (i.e. equilibrium points of the flow), and all of them are hyperbolic equilibrium points.
2. X has only a finite number of periodic orbits, and all of them are hyperbolic periodic orbits.
3. The limit sets of all orbits of X tends to a singular point or a periodic orbit.
4. The stable and unstable manifolds of the singular points and periodic orbits intersect transversely. In other words, if ${\displaystyle x_{i}}$ is a singular point (or periodic orbit) and ${\displaystyle W_{s}(x_{i})}$ (respectively, ${\displaystyle W_{u}(x_{i})}$) its stable (respectively, unstable) manifold, then ${\displaystyle w\in W_{s}(x_{i})\cap W_{u}(x_{j})}$ implies that the corresponding tangent spaces of the stable and unstable manifold satisfy ${\displaystyle T_{w}(W_{s}(x_{i}))+T_{w}(W_{u}(x_{j}))=T_{w}(M)}$.

Flow lines on an upright torus: the stable and unstable manifolds of the saddle points do not intersect transversely, so the height function does not satisfy the Morse-Smale condition.

Flow lines on a tilted torus: the height function satisfies the Morse-Smale condition.

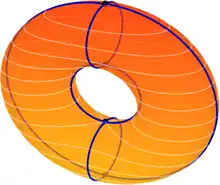
• Any Morse function f on a compact Riemannian manifold M defines a gradient vector field. If one imposes the condition that the unstable and stable manifolds of the critical points intersect transversely, then the gradient vector field and the corresponding smooth flow form a Morse–Smale system. The finite set of critical points of f forms the non-wandering set, which consists entirely of fixed points.
• Gradient-like dynamical systems are a particular case of Morse–Smale systems.
• For Morse–Smale systems on the 2D-sphere all equilibrium points and periodical orbits are hyperbolic; there are no separatrice loops.

• By Peixoto's theorem, the vector field on a 2D manifold is structurally stable if and only if this field is Morse-Smale.
• Consider a Morse-Smale system defined on compact differentiable manifold M with dimension n, and let the index of an equilibrium point (or a periodic orbit) be defined as the dimension of its associated unstable manifold. In Morse-Smale systems, the indices of the equilibrium points (and periodic orbits) are related with the topology of M by the Morse-Smale inequalities. Precisely, define m_i as the sum of the number of equilibrium points with index i and the number of periodic orbits with indices i and i + 1, and b_i as the i-th Betti number of M. Then the following inequalities are valid:[1]

${\displaystyle \sum _{j=0}^{i}(-1)^{j}m_{i-j}\geq \sum _{j=0}^{i}(-1)^{j}b_{i-j},\quad i=0,\ldots ,n}$

• D. V. Anosov (2001) [1994], "Morse–Smale system", Encyclopedia of Mathematics, EMS Press
• Dr. Michael Shub (ed.). "Morse-Smale systems". Scholarpedia.