n-curve
We take the functional theoretic algebra C[0, 1] of curves. For each loop γ at 1, and each positive integer n, we define a curve called n-curve. The n-curves are interesting in two ways.
- Their f-products, sums and differences give rise to many beautiful curves.
- Using the n-curves, we can define a transformation of curves, called n-curving.
Multiplicative inverse of a curve
A curve γ in the functional theoretic algebra C[0, 1], is invertible, i.e.
exists if
If , where , then
The set G of invertible curves is a non-commutative group under multiplication. Also the set H of loops at 1 is an Abelian subgroup of G. If , then the mapping is an inner automorphism of the group G.
We use these concepts to define n-curves and n-curving.
n-curves and their products
If x is a real number and [x] denotes the greatest integer not greater than x, then
If and n is a positive integer, then define a curve by
is also a loop at 1 and we call it an n-curve. Note that every curve in H is a 1-curve.
Suppose Then, since .
Example 1: Product of the astroid with the n-curve of the unit circle
Let us take u, the unit circle centered at the origin and α, the astroid. The n-curve of u is given by,
and the astroid is
The parametric equations of their product are
See the figure.
Since both are loops at 1, so is the product.
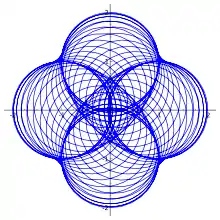 n-curve with |
 Animation of n-curve for n values from 0 to 50 |
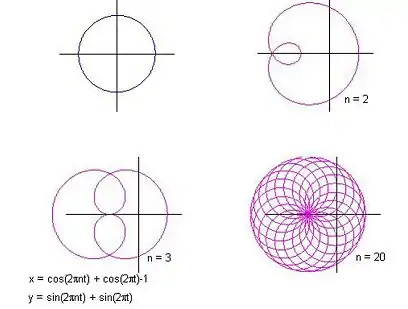
Example 2: Product of the unit circle and its n-curve
The unit circle is
and its n-curve is
The parametric equations of their product
are
See the figure.
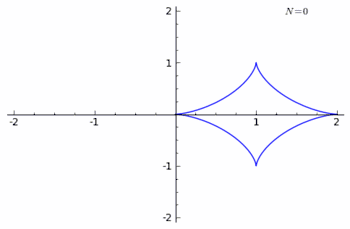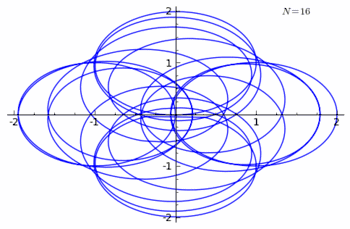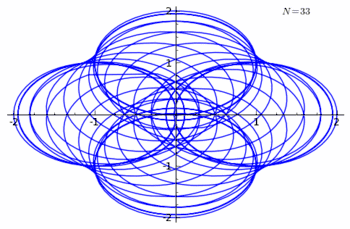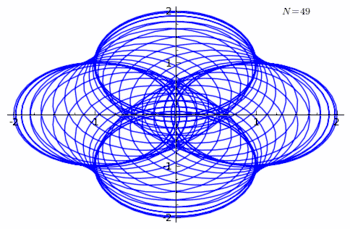
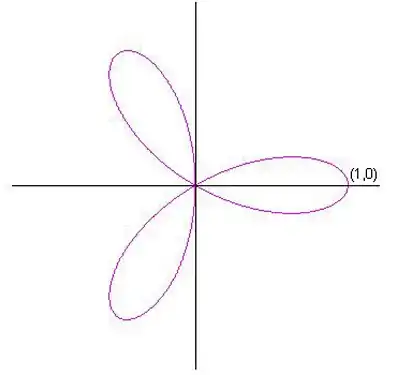
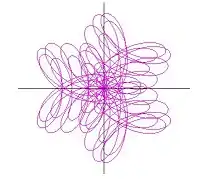
Example 3: n-Curve of the Rhodonea minus the Rhodonea curve
Let us take the Rhodonea Curve
If denotes the curve,
The parametric equations of are
n-Curving
If , then, as mentioned above, the n-curve . Therefore, the mapping is an inner automorphism of the group G. We extend this map to the whole of C[0, 1], denote it by and call it n-curving with γ. It can be verified that
This new curve has the same initial and end points as α.
Example 1 of n-curving
Let ρ denote the Rhodonea curve , which is a loop at 1. Its parametric equations are
With the loop ρ we shall n-curve the cosine curve
The curve has the parametric equations
See the figure.
It is a curve that starts at the point (0, 1) and ends at (2π, 1).
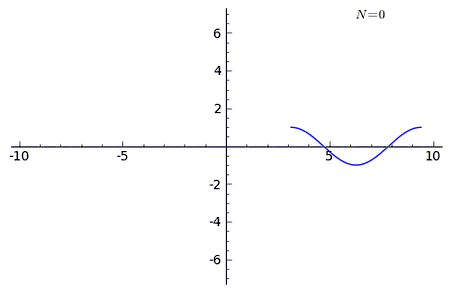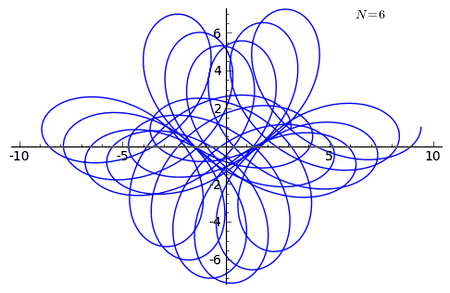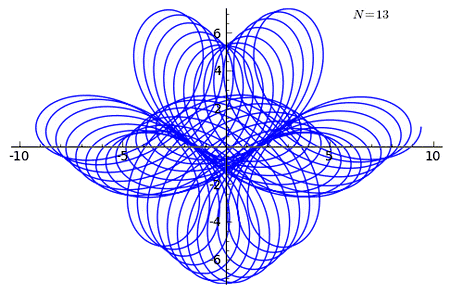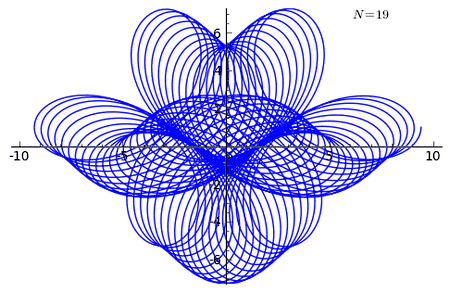
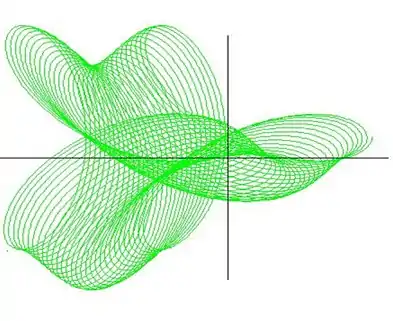
Example 2 of n-curving
Let χ denote the Cosine Curve
With another Rhodonea Curve
we shall n-curve the cosine curve.
The rhodonea curve can also be given as
The curve has the parametric equations
See the figure for .
Generalized n-curving
In the FTA C[0, 1] of curves, instead of e we shall take an arbitrary curve , a loop at 1. This is justified since
Then, for a curve γ in C[0, 1],
and
If , the mapping
given by
is the n-curving. We get the formula
Thus given any two loops and at 1, we get a transformation of curve
- given by the above formula.
This we shall call generalized n-curving.
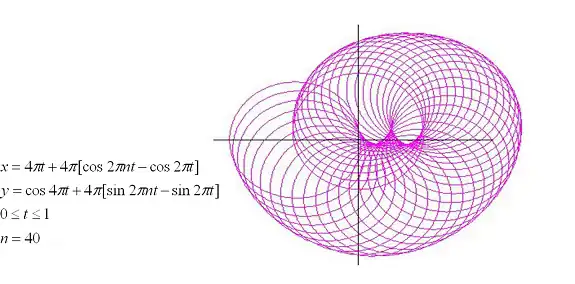
Example 1
Let us take and as the unit circle ``u.’’ and as the cosine curve
Note that
For the transformed curve for , see the figure.
The transformed curve has the parametric equations
Example 2
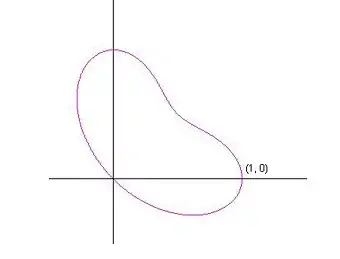
Denote the curve called Crooked Egg by whose polar equation is
Its parametric equations are
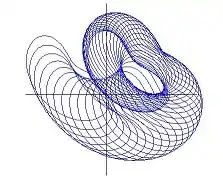
Let us take and
where is the unit circle.
The n-curved Archimedean spiral has the parametric equations
See the figures, the Crooked Egg and the transformed Spiral for .
References
- Sebastian Vattamattam, "Transforming Curves by n-Curving", in Bulletin of Kerala Mathematics Association, Vol. 5, No. 1, December 2008
- Sebastian Vattamattam, Book of Beautiful Curves, Expressions, Kottayam, January 2015 Book of Beautiful Curves