Natural neighbor interpolation

Natural neighbor interpolation is a method of spatial interpolation, developed by Robin Sibson.[1] The method is based on Voronoi tessellation of a discrete set of spatial points. This has advantages over simpler methods of interpolation, such as nearest-neighbor interpolation, in that it provides a smoother approximation to the underlying "true" function.

Natural neighbor interpolation with Sibson weights. The area of the green circles are the interpolating weights, w_i. The purple-shaded region is the new Voronoi cell, after inserting the point to be interpolated (black dot). The weights represent the intersection areas of the purple-cell with each of the seven surrounding cells.

The basic equation is:

${\displaystyle G(x)=\sum _{i=1}^{n}{w_{i}(x)f(x_{i})}}$

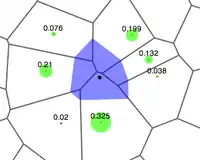
where ${\displaystyle G(x)}$ is the estimate at ${\displaystyle x}$, ${\displaystyle w_{i}}$ are the weights and ${\displaystyle f(x_{i})}$ are the known data at ${\displaystyle (x_{i})}$. The weights, ${\displaystyle w_{i}}$, are calculated by finding how much of each of the surrounding areas is "stolen" when inserting ${\displaystyle x}$ into the tessellation.

Sibson weights

${\displaystyle w_{i}(\mathbf {x} )={\frac {A(\mathbf {x} _{i})}{A(\mathbf {x} )}}}$

where A(x) is the volume of the new cell centered in x, and A(x_i) is the volume of the intersection between the new cell centered in x and the old cell centered in x_i.

Natural neighbor interpolation with Laplace weights. The interface l(x_i) between the cells linked to x and x_i is in blue, while the distance d(x_i) between x and x_i is in red.

Laplace weights[2][3]

${\displaystyle w_{i}(\mathbf {x} )={\frac {\frac {l(\mathbf {x} _{i})}{d(\mathbf {x} _{i})}}{\sum _{k=1}^{n}{\frac {l(\mathbf {x} _{k})}{d(\mathbf {x} _{k})}}}}}$

where l(x_i) is the measure of the interface between the cells linked to x and x_i in the Voronoi diagram (length in 2D, surface in 3D) and d(x_i), the distance between x and x_i.