Negative frequency

In mathematics, signed frequency (negative and positive frequency) expands upon the concept of frequency, from just an absolute value representing how often some repeating event occurs, to also have a positive or negative sign representing one of two opposing orientations for occurrences of those events. The following examples help illustrate the concept:

For a rotating object, the absolute value of its frequency of rotation indicates how many rotations the object completes per unit of time, while the sign could indicate whether it is rotating clockwise or counterclockwise.
- Mathematically speaking, the vector $(\cos(t),\sin(t))$ has a positive frequency of +1 radian per unit of time and rotates counterclockwise around the unit circle, while the vector $(\cos(-t),\sin(-t))$ has a negative frequency of -1 radian per unit of time, which rotates clockwise instead.
For a harmonic oscillator such as a pendulum, the absolute value of its frequency indicates how many times it swings back and forth per unit of time, while the sign could indicate in which of the two opposite directions it started moving.
For a periodic function represented in a Cartesian coordinate system, the absolute value of its frequency indicates how often in its domain it repeats its values, while changing the sign of its frequency could represent a reflection around its y-axis.

The counterclockwise-rotating vector

(cos t, sin t)

has a positive frequency of +1 radian per unit of time. Not shown is a clockwise-rotating vector

(cos - t, sin - t)

which has a negative frequency of -1 radian per unit of time. Both go around the unit circle every

2 π

units of time, but in opposite directions.

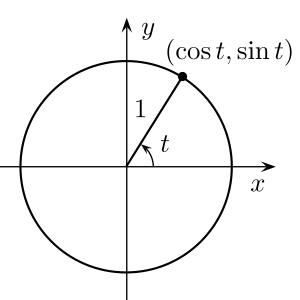
Sinusoids

Let $\omega$ be a nonnegative angular frequency with units of radians per unit of time and let $\varphi$ be a phase in radians. A function $\theta (t)=-\omega t+\varphi$ has slope $-\omega .$ When used as the argument of a sinusoid, $-\omega$ can represent a negative frequency.

Because cosine is an even function, the negative frequency sinusoid $\cos(-\omega t+\varphi )$ is indistinguishable from the positive frequency sinusoid $\cos(\omega t-\varphi ).$

Similarly, because sine is an odd function, the negative frequency sinusoid $\sin(-\omega t+\varphi )$ is indistinguishable from the positive frequency sinusoid ${\text{-}}\sin(\omega t-\varphi )$ or $\sin(\omega t-\varphi +\pi ).$

Thus any sinusoid can be represented in terms of positive frequencies only.

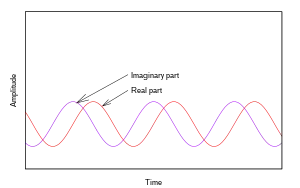
A negative frequency causes the sin function (violet) to lead the cos (red) by 1/4 cycle.

The sign of the underlying phase slope is ambiguous. Because $\cos(\omega t+\varphi )$ leads $\sin(\omega t+\varphi )$ by ${\tfrac {\pi }{2}}$ radians (or 1/4 cycle) for positive frequencies and lags by the same amount for negative frequencies, the ambiguity about the phase slope is resolved simply by observing a cosine and sine operator simultaneously and seeing which one leads the other.

The sign of $\omega$ is also preserved in the complex-valued function:

$e^{i\omega t}=\underbrace {\cos(\omega t)} _{R(t)}+i\cdot \underbrace {\sin(\omega t)} _{I(t)},$ [upper-alpha 1]

(Eq.1)

since $R(t)$ and $I(t)$ can be separately observed and compared. A common interpretation is that $e^{i\omega t}$ is a simpler function than either of its components, because it simplifies multiplicative trigonometric calculations, which leads to its formal description as the analytic representation of $\cos(\omega t)$ .[upper-alpha 2]

The sum of an analytic representation with its complex conjugate extracts the actual real-valued function they represent. For instance:

$\cos(\omega t)={\begin{matrix}{\frac {1}{2}}\end{matrix}}\left(e^{i\omega t}+e^{-i\omega t}\right),$

(Eq.2)

which gives rise to the somewhat misleading interpretation that $\cos(\omega t)$ comprises both a positive and a negative frequency. But the "sum" involves a cancellation of all imaginary components $({\tfrac {1}{2}}i\sin(\omega t)-{\tfrac {1}{2}}i\sin(\omega t))$ . That cancellation merely results in an ambiguity about the sign of the frequency. Using either sign provides an equivalent representation of the same cosine wave.

In any measure that indicates both frequencies, one of the two frequencies is a false positive or alias of the other, because $\omega$ can have only one sign.[upper-alpha 3] The Fourier transform, for instance, merely tells us that $\cos(\omega t)$ cross-correlates equally well with $\cos(\omega t)+i\sin(\omega t)$ as with $\cos(\omega t)-i\sin(\omega t).$ [upper-alpha 4] Nevertheless, treating a real sinusoid as the combination of a positive and a negative frequency is sometimes useful (and mathematically valid).

Applications

Simplifying the Fourier transform

Perhaps the best-known application of negative frequency is the formula:

{\hat {f}}(\omega )=\int _{-\infty }^{\infty }f(t)e^{-i\omega t}dt,

which is a measure of the energy in function $f(t)$ at frequency $\omega .$ When evaluated for a continuum of argument $\omega ,$ the result is called the Fourier transform.[upper-alpha 5]

For instance, consider the function:

f(t)=A_{1}e^{i\omega _{1}t}+A_{2}e^{i\omega _{2}t},\ \forall \ t\in \mathbb {R} ,\ \omega _{1}>0,\ \omega _{2}>0.

And:

{\begin{aligned}{\hat {f}}(\omega )&=\int _{-\infty }^{\infty }[A_{1}e^{i\omega _{1}t}+A_{2}e^{i\omega _{2}t}]e^{-i\omega t}dt\\&=\int _{-\infty }^{\infty }A_{1}e^{i\omega _{1}t}e^{-i\omega t}dt+\int _{-\infty }^{\infty }A_{2}e^{i\omega _{2}t}e^{-i\omega t}dt\\&=\int _{-\infty }^{\infty }A_{1}e^{i(\omega _{1}-\omega )t}dt+\int _{-\infty }^{\infty }A_{2}e^{i(\omega _{2}-\omega )t}dt\end{aligned}}

Note that although most functions do not comprise infinite duration sinusoids, that idealization is a common simplification that facilitates understanding.

Looking at the first term of this result, when $\omega =\omega _{1},$ the negative frequency $-\omega _{1}$ cancels the positive frequency, leaving just the constant coefficient $A_{1}$ (because $e^{i0t}=e^{0}=1$ ), which causes the infinite integral to diverge. At other values of $\omega$ the residual oscillations cause the integral to converge to zero. This idealized Fourier transform is usually written as:

{\hat {f}}(\omega )=2\pi A_{1}\delta (\omega -\omega _{1})+2\pi A_{2}\delta (\omega -\omega _{2}).

For realistic durations, the divergences and convergences are less extreme, and smaller non-zero convergences (spectral leakage) appear at many other frequencies, but the concept of negative frequency still applies. Fourier's original formulation (the sine transform and the cosine transform) requires an integral for the cosine and another for the sine. And the resultant trigonometric expressions are often less tractable than complex exponential expressions. (see Analytic signal, Euler's formula § Relationship to trigonometry, and Phasor)

Sampling of positive and negative frequencies and aliasing

This figure depicts two complex sinusoids, colored gold and cyan, that fit the same sets of real and imaginary sample points. They are thus aliases of each other when sampled at the rate (f_s) indicated by the grid lines. The gold-colored function depicts a positive frequency, because its real part (the cos function) leads its imaginary part by 1/4 of one cycle. The cyan function depicts a negative frequency, because its real part lags the imaginary part.

Notes

The equivalence is called Euler's formula
See Euler's formula § Relationship to trigonometry and Phasor § Addition for examples of calculations simplified by the complex representation.
Conversely, any measure that indicates only one frequency has made an assumption, perhaps based on collateral information.
cos(ωt) and sin(ωt) are orthogonal functions, so the imaginary parts of both correlations are zero.
There are several forms of the Fourier transform. This is the non-unitary form in angular frequency of time