Newton's cannonball

Newton's cannonball was a thought experiment Isaac Newton used to hypothesize that the force of gravity was universal, and it was the key force for planetary motion. It appeared in his posthumously published 1728 work De mundi systemate (also published in English as A Treatise of the System of the World).[1][2]

A cannon on top of a very high mountain shoots a cannonball horizontally. If the speed is low, the cannonball quickly falls back to Earth (A, B). At intermediate speeds, it will revolve around Earth along an elliptical orbit (C, D). Beyond the escape velocity, it will leave the Earth without returning (E).

Source

Newton's original plan for Philosophiæ Naturalis Principia Mathematica was that it should consist of two books, the first analyzing basic laws of motion, and the second applying them to the Solar System. In order to include more material on motion in resisting media, the first book was split into two; the succeeding (now third) book, originally written in a more popular style, was rewritten to be more mathematical.[3][4] However, manuscripts of an earlier draft of this last book survived, and a version of it was published in 1728 as De mundi systemate; an English translation was also published earlier in 1728 under the name A Treatise of the System of the World.[1][2][4] The thought experiment occurs near the start of this work.

Animation

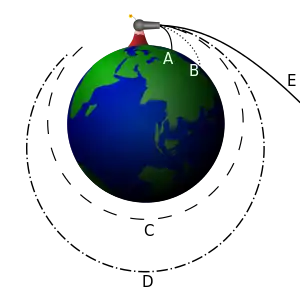
In this experiment from his book (pp. 5–8),[2] Newton visualizes a stone (you could also use a cannonball) being projected on top of a very high mountain. If there were no forces of gravitation or air resistance, the body should follow a straight line away from Earth, in the direction that it was projected. If a gravitational force acts on the projectile, it will follow a different path depending on its initial velocity. If the speed is low, it will simply fall back on Earth. (A and B) for example horizontal speed of 0 to 7,000 m/s for Earth.

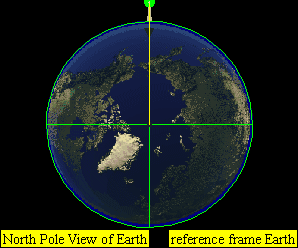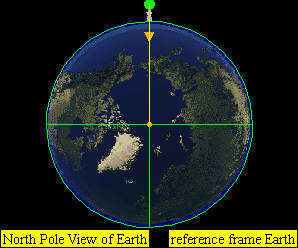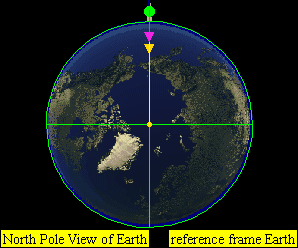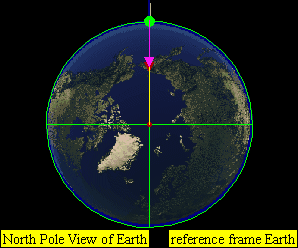
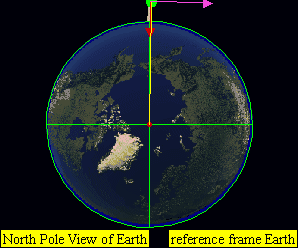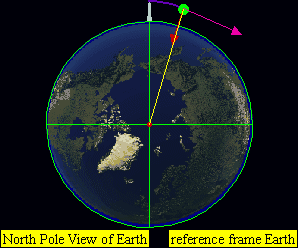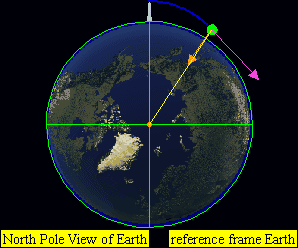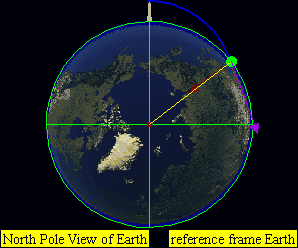
Speed of cannonball at 0 m/s launched horizontally from Newton's very tall mountain.
Speed of cannonball at 6,000 m/s launched horizontally from Newton's very tall mountain.

If the speed is the orbital speed at that altitude, it will go on circling around the Earth along a fixed circular orbit. (C) for example horizontal speed of at approximately 7,800 m/s for Earth.

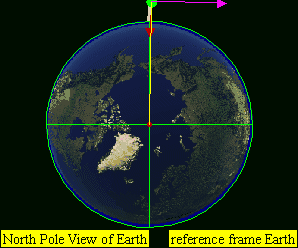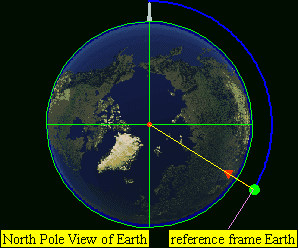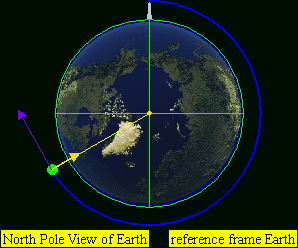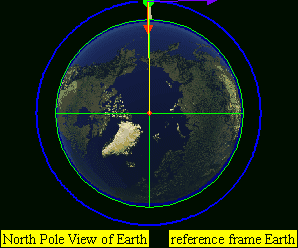
Speed of cannonball at 7,300 m/s launched horizontally from Newton's very tall mountain.

If the speed is higher than the orbital velocity, but not high enough to leave Earth altogether (lower than the escape velocity), it will continue revolving around Earth along an elliptical orbit. (D) for example horizontal speed of 7,800 to approximately 11,200 m/s for Earth.

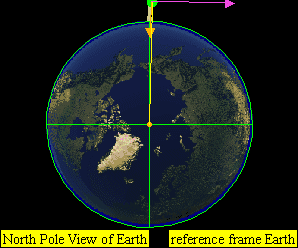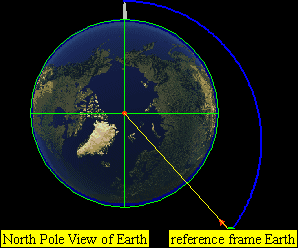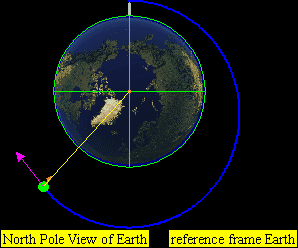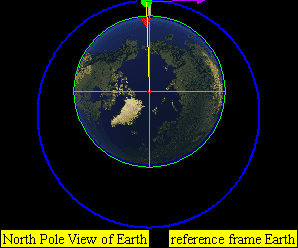
Speed of cannonball at 8,000 m/s launched horizontally from Newton's very tall mountain.

If the speed is very high, it will leave Earth in a parabolic (at exactly escape velocity) or hyperbolic trajectory. (E) for example horizontal speed of approximately greater than 11,200 m/s for Earth.

Speed of cannonball at 11,200 m/s launched horizontally from Newton's very tall mountain.

Other appearances

An image of the page from A Treatise of the System of the World showing Newton's diagram of this experiment was included on the Voyager Golden Record[5] (image #111).

This is a photograph of page 6 from Newton's De mundi systemate (A Treatise of the System of the World). It is part of the image collection on the Voyager Golden Record that is being carried into deep space aboard the Voyager 1 and 2 spacecraft.

See also

Notes
  1. De mundi systemate, Isaac Newton, London: J. Tonson, J. Osborn, & T. Longman, 1728.
  2. A Treatise of the System of the World, Isaac Newton, London: printed for F. Fayram, 1728.
  3. Newton’s Philosophiae Naturalis Principia Mathematica, George Smith, 2007, Stanford Encyclopedia of Philosophy. Retrieved 14 September 2021.
  4. A Treatise of the System of the World, Isaac Newton, introd. I. Bernard Cohen, Dover Phoenix Editions, 2004, ISBN 0-486-43880-5.
  5. Sagan, Carl et al. (1978) Murmurs of Earth: The Voyager Interstellar Record. New York: Random House. ISBN 0-394-41047-5 (hardcover), ISBN 0-345-28396-1 (paperback)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.