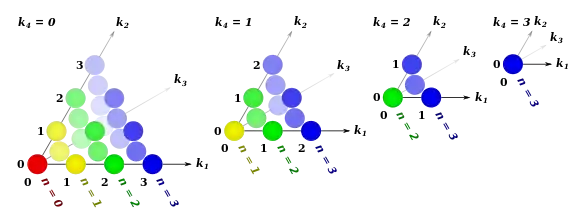Pascal's simplex
In mathematics, Pascal's simplex is a generalisation of Pascal's triangle into arbitrary number of dimensions, based on the multinomial theorem.
Generic Pascal's m-simplex
Let m (m > 0) be a number of terms of a polynomial and n (n ≥ 0) be a power the polynomial is raised to.
Let denote a Pascal's m-simplex. Each Pascal's m-simplex is a semi-infinite object, which consists of an infinite series of its components.
Let denote its nth component, itself a finite (m − 1)-simplex with the edge length n, with a notational equivalent .
nth component
consists of the coefficients of multinomial expansion of a polynomial with m terms raised to the power of n:
where .
Specific Pascal's simplices
Pascal's 1-simplex
is not known by any special name.
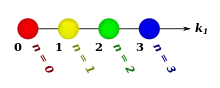
nth component
(a point) is the coefficient of multinomial expansion of a polynomial with 1 term raised to the power of n:
Arrangement of
which equals 1 for all n.
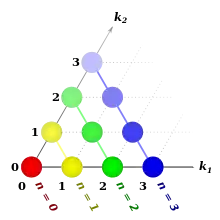
nth component
(a line) consists of the coefficients of binomial expansion of a polynomial with 2 terms raised to the power of n:
Arrangement of
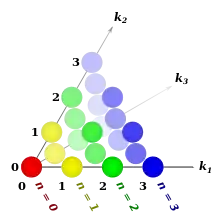
nth component
(a triangle) consists of the coefficients of trinomial expansion of a polynomial with 3 terms raised to the power of n:
Arrangement of
Properties
Inheritance of components
is numerically equal to each (m − 1)-face (there is m + 1 of them) of , or:
From this follows, that the whole is (m + 1)-times included in , or:
Example
1 |
1 |
1 |
1 | |
1 |
1 1 |
1 1 1 |
1 1 1 1 | |
1 |
1 2 1 |
1 2 1 2 2 1 |
1 2 1 2 2 1 2 2 2 1 | |
1 |
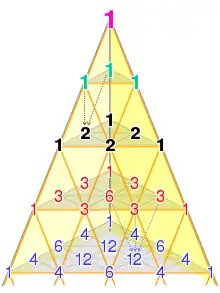
1 3 3 1 |
1 3 3 1 3 6 3 3 3 1 |
1 3 3 1 3 6 3 3 3 1 3 6 3 6 6 3 3 3 3 1 |
For more terms in the above array refer to (sequence A191358 in the OEIS)
Equality of sub-faces
Conversely, is (m + 1)-times bounded by , or:
From this follows, that for given n, all i-faces are numerically equal in nth components of all Pascal's (m > i)-simplices, or:
Example
The 3rd component (2-simplex) of Pascal's 3-simplex is bounded by 3 equal 1-faces (lines). Each 1-face (line) is bounded by 2 equal 0-faces (vertices):
2-simplex 1-faces of 2-simplex 0-faces of 1-face
1 3 3 1 1 . . . . . . 1 1 3 3 1 1 . . . . . . 1
3 6 3 3 . . . . 3 . . .
3 3 3 . . 3 . .
1 1 1 .
Also, for all m and all n:
Number of coefficients
For the nth component ((m − 1)-simplex) of Pascal's m-simplex, the number of the coefficients of multinomial expansion it consists of is given by:
(where the latter is the multichoose notation). We can see this either as a sum of the number of coefficients of an (n − 1)th component ((m − 1)-simplex) of Pascal's m-simplex with the number of coefficients of an nth component ((m − 2)-simplex) of Pascal's (m − 1)-simplex, or by a number of all possible partitions of an nth power among m exponents.
Example
| m-simplex | nth component | n = 0 | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 |
|---|---|---|---|---|---|---|---|
| 1-simplex | 0-simplex | 1 | 1 | 1 | 1 | 1 | 1 |
| 2-simplex | 1-simplex | 1 | 2 | 3 | 4 | 5 | 6 |
| 3-simplex | 2-simplex | 1 | 3 | 6 | 10 | 15 | 21 |
| 4-simplex | 3-simplex | 1 | 4 | 10 | 20 | 35 | 56 |
| 5-simplex | 4-simplex | 1 | 5 | 15 | 35 | 70 | 126 |
| 6-simplex | 5-simplex | 1 | 6 | 21 | 56 | 126 | 252 |
The terms of this table comprise a Pascal triangle in the format of a symmetric Pascal matrix.
Symmetry
An nth component ((m − 1)-simplex) of Pascal's m-simplex has the (m!)-fold spatial symmetry.
Geometry
Orthogonal axes in m-dimensional space, vertices of component at n on each axis, the tip at [0,...,0] for .
Numeric construction
Wrapped n-th power of a big number gives instantly the n-th component of a Pascal's simplex.
where .