Percus–Yevick approximation

The direct correlation function represents the direct correlation between two particles in a system containing N − 2 other particles. It can be represented by

${\displaystyle c(r)=g_{\rm {total}}(r)-g_{\rm {indirect}}(r)\,}$

where ${\displaystyle g_{\rm {total}}(r)}$ is the radial distribution function, i.e. ${\displaystyle g(r)=\exp[-\beta w(r)]}$ (with w(r) the potential of mean force) and ${\displaystyle g_{\rm {indirect}}(r)}$ is the radial distribution function without the direct interaction between pairs ${\displaystyle u(r)}$ included; i.e. we write ${\displaystyle g_{\rm {indirect}}(r)=\exp[-\beta (w(r)-u(r))]}$. Thus we approximate c(r) by

${\displaystyle c(r)=e^{-\beta w(r)}-e^{-\beta [w(r)-u(r)]}.\,}$

If we introduce the function ${\displaystyle y(r)=e^{\beta u(r)}g(r)}$ into the approximation for c(r) one obtains

${\displaystyle c(r)=g(r)-y(r)=e^{-\beta u}y(r)-y(r)=f(r)y(r).\,}$

This is the essence of the Percus–Yevick approximation for if we substitute this result in the Ornstein–Zernike equation, one obtains the Percus–Yevick equation:

${\displaystyle y(r_{12})=1+\rho \int f(r_{13})y(r_{13})h(r_{23})d\mathbf {r_{3}} .\,}$

The approximation was defined by Percus and Yevick in 1958.

Static structure factor of the hard-spheres liquid in Percus-Yevick approximation at three different packing ratios.

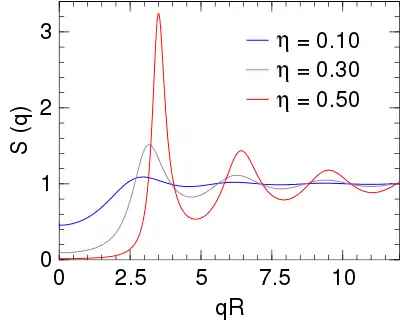
For hard spheres, the potential u(r) is either zero or infinite, and therefore the Boltzmann factor ${\displaystyle {\text{e}}^{-u/k_{\text{B}}T}}$ is either one or zero, regardless of temperature T. Therefore structure of a hard-spheres fluid is temperature independent. This leaves just two parameters: the hard-core radius R (which can be eliminated by rescaling distances or wavenumbers), and the packing fraction η (which has a maximum value of 0.64 for random close packing).

Under these conditions, the Percus-Yevick equation has an analytical solution, obtained by Wertheim in 1963.[2][3][4]

double py(double qr, double eta)
{
    const double a = pow(1+2*eta, 2)/pow(1-eta, 4);
    const double b = -6*eta*pow(1+eta/2, 2)/pow(1-eta, 4);
    const double c = eta/2*pow(1+2*eta, 2)/pow(1-eta, 4);
    const double A = 2*qr;
    const double A2 = A*A;
    const double G = a/A2*(sin(A)-A*cos(A))
        + b/A/A2*(2*A*sin(A)+(2-A2)*cos(A)-2)
        + c/pow(A,5)*(-pow(A,4)*cos(A)+4*((3*A2-6)*cos(A)+A*(A2-6)*sin(A)+6));

    return 1/(1+24*eta*G/A);
}

For hard spheres in shear flow, the function u(r) arises from the solution to the steady-state two-body Smoluchowski convection-diffusion equation or two-body Smoluchowski equation with shear flow. An approximate analytical solution to the Smoluchowski convection-diffusion equation was found using the method of matched asymptotic expansions by Banetta and Zaccone in Ref.[5]

This analytical solution can then be used together with the Percus-Yevick approximation in the Ornstein-Zernike equation. Approximate solutions for the pair distribution function in the extensional and compressional sectors of shear flow and hence the angular-averaged radial distribution function can be obtained, as shown in Ref.[6], which are in good parameter-free agreement with numerical data up to packing fractions ${\displaystyle \eta \approx 0.5}$.

• Hypernetted chain equation — another closure relation
• Ornstein–Zernike equation