Perfect graph
In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

The perfect graphs include many important families of graphs and serve to unify results relating colorings and cliques in those families. For instance, in all perfect graphs, the graph coloring problem, maximum clique problem, and maximum independent set problem can all be solved in polynomial time, despite their greater complexity for non-perfect graphs. In addition, several important minimax theorems in combinatorics, including Dilworth's theorem and Mirsky's theorem on partially ordered sets, Kőnig's theorem on matchings, and the Erdős–Szekeres theorem on monotonic sequences, can be expressed in terms of the perfection of certain associated graphs.
The perfect graph theorem states that the complement graph of a perfect graph is also perfect. The strong perfect graph theorem characterizes the perfect graphs in terms of certain forbidden induced subgraphs, leading to a polynomial time algorithm for testing whether a graph is perfect.
Definitions and characterizations
A clique in an undirected graph is a subset of its vertices that are all adjacent to each other. A graph coloring assigns a color to each vertex so that each two adjacent vertices have different colors. In particular, the vertices of any clique must all be assigned different colors, so the chromatic number (the minimum number of colors in any coloring) is always greater than or equal to the clique number, the number of vertices in the maximum clique. The perfect graphs are defined as the graphs for which these two numbers are equal, not just in the graph itself, but in every induced subgraph obtained by deleting some of its vertices.[1]

The perfect graph theorem asserts that the complement graph of a perfect graph is itself perfect. The complement graph has the same vertices as the given graph, but a complementary adjacency relation: two vertices are adjacent, in the complement graph, if and only if they are not adjacent in the given graph. A clique, in the complement graph, corresponds to an independent set in the given. A coloring of the complement graph corresponds to a clique cover, a partition of the vertices of the given graph into cliques. The fact that the complement of a perfect graph is also perfect implies that, in itself, the independence number (the size of its maximum independent set), equals its clique cover number (the fewest number of cliques needed in a clique cover). More strongly, the same thing is true in every induced subgraph of the complement graph. This provides an alternative and equivalent definition of the perfect graphs: they are the graphs for which, in each induced subgraph, the independence number equals the clique cover number.[2]
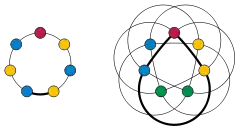
The strong perfect graph theorem gives a different way of defining perfect graphs, by their structure instead of by their properties. It is based on the existence of cycle graphs and their complements among the induced subgraphs of a given graph. A cycle of odd length, greater than three, is not a perfect graph: its clique number is two, but its chromatic number is three. By the perfect graph theorem, the complement of an odd cycle of length greater than three is also not perfect. The complement of a length-5 cycle is another length-5 cycle, but for larger odd lengths the complement is not a cycle. The strong perfect graph theorem asserts that these are the only forbidden induced subgraphs for the perfect graphs: a graph is perfect if and only if its induced subgraphs include neither an odd cycle nor an odd anticycle of five or more vertices. In this context, induced cycles that are not triangles are called "holes", and their complements are called "antiholes", so the strong perfect graph theorem can be stated more succinctly: a graph is perfect if and only if it has neither an odd hole nor an odd antihole.[3]
These results can be combined in another characterization of perfect graphs: they are the graphs for which the product of the clique number and independence number is greater than or equal to the number of vertices, and for which the same is true for all induced subgraphs. Because the statement of this characterization remains invariant under complementation of graphs, it implies the perfect graph theorem. One direction of this characterization follows easily from the original definition of perfect: the number of vertices in any graph equals the sum of the sizes of the color classes in an optimal coloring, and is less than or equal to the number of colors multiplied by the independence number. In a perfect graph, the number of colors equals the clique number, and can be replaced by the clique number in this inequality.[4] The other direction follows from the strong perfect graph theorem and the observation that in odd cycles of length greater than three the product of the clique number and independence number is one less than the number of vertices.
History
The theory of perfect graphs developed from a 1958 result of Tibor Gallai that in modern language can be interpreted as stating that the complement of a bipartite graph is perfect;[5] this result can also be viewed as a simple equivalent of Kőnig's theorem, a much earlier result relating matchings and vertex covers in bipartite graphs. The first formulation of the concept of perfect graphs more generally was in a 1961 paper by Claude Berge, in German,[6] and the first use of the phrase "perfect graph" appears to be in a 1963 paper of Berge.[7] In these works he unified Gallai's result with several similar results by defining perfect graphs, and he conjectured both the perfect graph theorem and the strong perfect graph theorem. In formulating these concepts, Berge was motivated by the concept of the Shannon capacity of a graph, by the fact that for (co-)perfect graphs it equals the independence number, and by the search for minimal examples of graphs for which this is not the case.[8] Until the strong perfect graph theorem was proven, the graphs described by it (that is, the graphs with no odd hole and no odd antihole) were called Berge graphs.[9]
The perfect graph theorem was proven by László Lovász in 1972,[2] who in the same year proved the stronger inequality between the number of vertices and the product of the clique number and independence number, without benefit of the strong perfect graph theorem.[4] In 1991, Alfred Lehman won Fulkerson Prize, sponsored jointly by the Mathematical Optimization Society and American Mathematical Society, for his work on generalizations of the theory of perfect graphs to logical matrices.[10] The conjectured strong perfect graph theorem became the focus of research in the theory of perfect graphs for many years,[9] until its proof was announced in 2002 by Maria Chudnovsky, Neil Robertson, Paul Seymour, and Robin Thomas,[11] and published by them in 2006.[3] This work won its authors the 2009 Fulkerson Prize.[12] The perfect graph theorem has a short proof, but the proof of the strong perfect graph theorem is long and technical, based on a deep structural decomposition of Berge graphs. Related decomposition techniques have also borne fruit in the study of other graph classes, and in particular for the claw-free graphs.[13] The symmetric characterization of perfect graphs in terms of the product of clique number and independence number was originally suggested by Hajnal and proven by Lovász.[4]
Families of graphs
Many well-studied families of graphs are perfect,[9] and in many cases the fact that these graphs are perfect corresponds to a minimax theorem for some kinds of combinatorial structure defined by these graphs. Examples of this phenomenon include the perfection of bipartite graphs and their line graphs, associated with Kőnig's theorem relating maximum matchings and vertex covers in bipartite graphs, and the perfection of comparability graphs, associated with Dilworth's theorem and Mirsky's theorem on chains and antichains in partially ordered sets. Other important classes of graphs, defined by having a structure related to the holes and antiholes of the strong perfect graph theorem, include the chordal graphs, Meyniel graphs, and their subclasses.
Bipartite graphs and line graphs
A bipartite graph is a graph that can be colored with two colors, or equivalently a graph that has no odd cycles. Because they have no odd cycles, they have no cliques of three or more vertices, so (when they have at least one edge) their chromatic number and clique number are both two. An induced subgraph of a bipartite graph remains bipartite, with the same equality between chromatic number and clique number, so the bipartite graphs are perfect.[9] They include as subclasses the trees, even-length cycle graphs, lattice graphs, knight's graphs, modular graphs, median graphs, and partial cubes, among many others.[14]
The perfect graph theorem, applied to bipartite graphs, produces a less-obvious equality: in these graphs, the size of the maximum independent set equals the size of the smallest clique cover. Because bipartite graphs are triangle-free, their minimum clique covers consist of a maximum matching (a set of disjoint edges, as many as possible) together with one-vertex cliques for all remaining vertices. And in any graph, the maximum independent set is complementary to a vertex cover, a set of vertices that touches all edges. Therefore, the equality of the maximum independent set and minimum clique cover can be expressed equivalently as an equality between the size of the maximum matching and the minimum vertex cover, the usual formulation of Kőnig's theorem.[15][16]
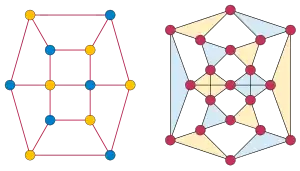
The same equality can be expressed in another way, involving a different class of perfect graphs. A matching, in any graph , is the same thing as an independent set in the line graph , a graph that has a vertex for each edge in . There is an edge between two vertices in whenever the corresponding two edges in share an endpoint. There are two kinds of cliques in a line graph : the ones coming from sets of edges in that all have a common endpoint, and the ones coming from triangles in . However, if is bipartite, only the first kind of clique can exist in . Therefore, in this case, a clique cover in corresponds to a vertex cover in , so in line graphs of bipartite graphs the independence number and clique cover number are equal. Induced subgraphs of line graphs of bipartite graphs remain in the same family (they correspond to the subgraphs of the underlying bipartite graph), and so the line graphs of bipartite graphs are perfect.[16] In particular this is true of the rook's graphs, the line graphs of complete bipartite graphs. Every line graph of a bipartite graph is an induced subgraph of a rook's graph.[17]
Because line graphs of bipartite graphs are perfect, their clique number equals their chromatic number. The clique number of the line graph of a bipartite graph is the maximum degree of any vertex of the underlying bipartite graph. The chromatic number of the line graph of a bipartite graph is the chromatic index of the underlying bipartite graph. It is the minimum number of colors needed to color the edges so that no two edges of the same color share an endpoint. Each color class forms a matching, so the chromatic index is also the minimum number of matchings needed to cover all of the edges of the graph. The equality of maximum degree and chromatic index, in bipartite graphs, is another theorem of Dénes Kőnig.[18] In arbitrary simple graphs, they can differ by one; this is Vizing's theorem.[16]
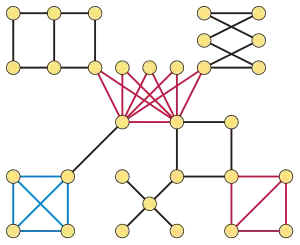
If a line graph is perfect, the underlying graph is said to be a line perfect graph. The line perfect graphs are the graphs whose biconnected components are bipartite graphs, the complete graph , and triangular books, sets of triangles sharing an edge. Because these components are themselves perfect, and are combined in a way that preserves the property of being perfect, every line perfect graph is itself a perfect graph.[16]
The bipartite graphs, their complements, and the line graphs of bipartite graphs and their complements form four basic classes of perfect graphs that play a key role in the proof of the strong perfect graph theorem. According to the structural decomposition of perfect graphs used as part of this proof, every perfect graph that is not already in one of these four classes can be decomposed by partitioning its vertices into subsets, in one of four ways, called a 2-join, the complement of a 2-join, a homogeneous pair, or a skew partition.[19]
Comparability graphs

A partially ordered set is defined by its set of elements, and a comparison relation on these elements, obeying the requirements that ≤ is a reflexive relation (for all elements , ), an antisymmetric relation (if and , then , and a transitive relation (if and , then ). Two distinct elements and are said to be comparable if or , and incomparable otherwise. For instance, the set inclusion operation is the comparison relation of a partial order on any family of sets. The comparability graph of a partially ordered set is a graph with the set elements as its vertices, and with an edge connecting two vertices whenever those two elements are comparable. Its complement is called an incomparability graph. The comparability graph is not enough to uniquely identify a partial order; different partial orders may have the same comparability graph. For instance, reversing all comparison relations between pairs of elements changes their order but does not change their comparability graph.[20]
Finite comparability graphs (and their complementary incomparability graphs) are always perfect.[21] A clique, in a comparability graph, comes from a subset of elements that are all pairwise comparable; such a subset is called a chain, and it is linearly ordered by the given partial order. An independent set comes from a subset of elements no two of which are comparable; such a subset is called an antichain. Thus, a coloring of a comparability graph is a partition of its elements into antichains, and a clique cover is a partition of its elements into chains. Dilworth's theorem, in the theory of partial orders, states that for every finite partial order, the size of the largest antichain equals the minimum number of chains into which the elements can be partitioned. In the language of graphs, this can be stated as: every finite comparability graph is perfect. Similarly, Mirsky's theorem states that for every finite partial order, the size of the largest chain equals the minimum number of antichains into which the elements can be partitioned, or that every finite incomparability graph is perfect. These two theorems are equivalent via the perfect graph theorem, but Mirsky's theorem is easier than Dilworth's theorem to prove directly: if each element is labeled by the size of the largest chain in which it is maximal, then the subsets with equal labels form a partition into antichains, with the number of antichains equal to the size of the largest chain overall.[22]
Every bipartite graph is the comparability graph of a partial order. If a bipartite graph has its vertices colored, say red and blue, then it is the comparability graph for a comparison relation in which every red vertex is every blue vertex, every vertex is itself, and there are no other comparable pairs. In the partial orders constructed in this way, the largest chains consist of one red and one blue vertex. Thus, by connecting them through the theory of perfect graphs, Kőnig's theorem can be seen as a special case of Dilworth's theorem.[23]
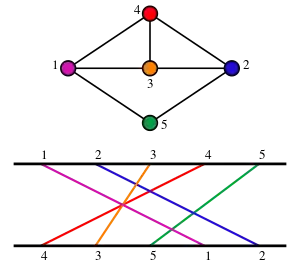
A permutation graph is defined from a permutation on a totally ordered sequence of elements (conventionally, the integers from to ), which form the vertices of the graph. The edges of a permutation graph connect pairs of elements whose ordering is reversed by the given permutation. These are naturally incomparability graphs, for a partial order in which whenever occurs before in both the given sequence and its permutation. The complement of a permutation graph is another permutation graph, for the reverse of the given permutation. Therefore, as well as being incomparability graphs, permutation graphs are comparability graphs. In fact, the permutation graphs are exactly the graphs that are both comparability and incomparability graphs.[24] A clique, in a permutation graph, is a subsequence of elements that appear in increasing order in the given permutation, and an independent set is a subsequence of elements that appear in decreasing order. In any perfect graph, the product of the clique number and independence number are at least the number of vertices; the special case of this inequality for permutation graphs is the Erdős–Szekeres theorem.[22]

The interval graphs are the incomparability graphs of interval orders, orderings defined by sets of intervals on the real line with whenever interval is completely to the left of interval . In the corresponding interval graph, there is an edge from to whenever the two intervals have a point in common. Coloring these graphs can be used to model problems of assigning resources to tasks (such as classrooms to classes) with intervals describing the scheduled time of each task.[25] Both interval graphs and permutation graphs are generalized by the trapezoid graphs, the incomparability graphs of orderings defined in the same way for a system of trapezoids between two parallel lines, with whenever trapezoid is completely to the left of trapezoid .[26] Systems of intervals in which no two are nested produce a more restricted class of graphs, the indifference graphs, the incomparability graphs of semiorders. These have been used to model human preferences under the assumption that, when items have utilities that are very close to each other, they will be incomparable.[27] Another special case of the interval graphs is the family of trivially perfect graphs, formed from intervals where each two are either nested or disjoint.[28] These are the comparability graphs of ordered trees, and the graphs for which, in every induced subgraph, the independence number equals the number of maximal cliques.[29]
Split graphs and random perfect graphs
A split graph is a graph that can be partitioned into a clique and an independent set. When the clique is chosen to be maximal, such a graph can be colored optimally by assigning one color to each clique vertex, and assigning each independent set vertex the color of a non-adjacent clique vertex. Therefore, these graphs have equal clique numbers and chromatic numbers, and are perfect.
A little more generally, the unipolar graphs are the graphs that can be partitioned into a clique and a cluster graph, a disjoint union of cliques. These include, for instance, the complements of bipartite graphs, as they can be partitioned into two cliques. The unipolar graphs and their complements together form the class of generalized split graphs. Almost all perfect graphs are generalized split graphs, in the sense that the fraction of perfect -vertex graphs that are generalized split graphs goes to one in the limit as grows arbitrarily large.[30]
It follows from this result that other limiting properties of almost all perfect graphs can be determined by studying the generalized split graphs. In this way, it has been shown that almost all perfect graphs contain a Hamiltonian cycle. If is an arbitrary graph, the limiting probability that occurs as an induced subgraph of a large random perfect graph is 0, 1/2, or 1, respectively as is not a generalized split graph, is unipolar or co-unipolar but not both, or is both unipolar and co-unipolar.[31]
Incremental constructions
Several families of perfect graphs can be characterized by an incremental construction in which the graphs in the family are built up by adding one vertex at a time, according to certain rules, which guarantee that after each vertex is added the graph remains perfect.
- The chordal graphs are the graphs formed by a construction of this type in which, at the time a vertex is added, its neighbors form a clique. The maximum clique in the graph is the largest clique obtained in this way from a newly added vertex and its neighbors. Chordal graphs may also be characterized as the graphs that have no holes (even or odd). They include as special cases the forests, the interval graphs, split graphs, and the maximal outerplanar graphs. The k-trees, central to the definition of treewidth, are chordal graphs in which all maximal cliques have the same size.
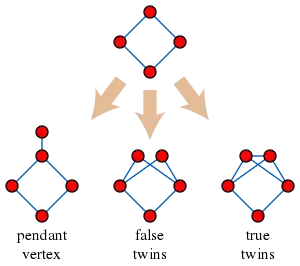
- The distance-hereditary graphs are formed, starting from a single-vertex graph, by repeatedly adding degree-one vertices ("pendant vertices") or copies of existing vertices (with the same neighbors). Each time a vertex is copied, the vertex and its copy may be adjacent (forming true twins) or non-adjacent (forming false twins). These graphs have the property that, in every connected induced subgraph, the distances between vertices are the same as in the whole graph. If only the twin operations are used, the result is a cograph.[32] The cographs are the comparability graphs of series-parallel partial orders[33] and can also be formed by a different construction process combining complementation and the disjoint union of graphs.[34]
- The graphs that are both chordal and distance-hereditary are called Ptolemaic graphs, because their distances obey Ptolemy's inequality.[35] They have a restricted form of the distance-hereditary construction sequence, in which a false twin can only be added when its neighbors would form a clique.[32] They include as special cases the windmill graphs consisting of cliques joined at a single vertex, and the block graphs in which each biconnected component is a clique.[35]
- The threshold graphs are formed from an empty graph by repeatedly adding either an isolated vertex (connected to nothing else) or a universal vertex (connected to all other vertices).[36] They are special cases of the split graphs and the trivially perfect graphs. They are exactly the graphs that are both trivially perfect and the complement of a trivially perfect graph; they are also exactly the graphs that are both cographs and split graphs.[37]
If the vertices of a chordal graph are colored in the order of an incremental construction sequence using a greedy coloring algorithm, the result will be an optimal coloring. The reverse of the vertex ordering used in this construction is called an elimination order. Similarly, if the vertices of a distance-hereditary graph are colored in the order of an incremental construction sequence, the resulting coloring will be optimal. If the vertices of a comparability graph are colored in the order of a linear extension of its underlying partial order, the resulting coloring will be optimal. This property is generalized in the family of perfectly orderable graphs, the graphs for which there exists an ordering that, when restricted to any induced subgraph, causes greedy coloring to be optimal. The cographs are exactly the graphs for which all vertex orderings have this property.
Other families
Many other classes of perfect graphs have been studied. For instance, the strongly perfect graphs are graphs in which, in every induced subgraph, there exists an independent set that intersects all maximal cliques. The Meyniel graphs have been called very strongly perfect because in them, every vertex belongs to such an independent set. The Meyniel graphs can also be defined as the graphs in which every odd cycle of length five or more has at least two chords.[38]

A parity graph is defined by the property that between every two vertices, all induced paths have the same parity: either they are all even in length, or they are all odd in length. This is true, for instance, of the distance-hereditary graphs, in which all induced paths between the same two vertices have the same length.[39] It is also true of the bipartite graphs: in a bipartite graph, if two vertices are on the same side of the bipartition, then all paths between them have even length, and if they are on opposite sides then all paths between them have odd length. The parity graphs are a subclass of the Meyniel graphs: in any long odd cycle of a parity graph, at least two chords are needed to prevent the cycle being partitioned into two induced paths of different parity. The prism over any parity graph (its Cartesian product with a single edge) is another parity graph, and the parity graphs are the only graphs whose prisms are perfect.[40]
Tolerance graphs are defined by specifying both an interval of the real line for each vertex and a non-negative real number, the tolerance of the vertex. Two vertices are adjacent whenever their intervals overlap for a length that is at least as large as the minimum of their two tolerances. Thus, the interval graphs are a special case of tolerance graphs, having tolerance zero. Like interval graphs, tolerance graphs can be used to model scheduling problems, where the tasks to be scheduled may only share resources for a short period of time (the tolerance of the tasks). The complements of tolerance graphs form a subclass of the perfectly orderable graphs.[41]
Matrices, polyhedra, and integer programming
Perfect graphs are closely connected to the theory of linear programming and integer programming. Both linear programs and integer programs are expressed in canonical form as seeking a vector that maximizes a linear objective function , subject to the linear constraints and . Here, is given as a matrix, and and are given as two vectors. Although linear programs and integer programs are specified in this same way, they differ in that, in a linear program, the solution vector is allowed to have arbitrary real numbers as its coefficients, whereas in an integer program these unknown coefficients must be integers. This makes a very big difference in the computational complexity of these problems: linear programming can be solved in polynomial time, but integer programming is NP-hard.[1]
When the same given values , , and are used to define both a linear program and an integer program, they commonly have different optimal solutions. The linear program is called an integral linear program if an optimal solution to the integer program is also optimal for the linear program. (Otherwise, the ratio between the two solution values is called the integrality gap, and is important in analyzing approximation algorithms for the integer program.) Perfect graphs may be used to characterize the (0, 1) matrices (that is, matrices where all coefficients are 0 or 1) with the following property: if is the all-ones vector, then for all choices of the resulting linear program is integral.[1]
As Václav Chvátal proved, every matrix with this property is (up to removal of irrelevant "dominated" rows) the maximal clique versus vertex incidence matrix of a perfect graph. This matrix has a column for each vertex of the graph, and a row for each maximal clique, with a coefficient that is one in the columns of vertices that belong to the clique and zero in the remaining columns. The integral linear programs encoded by this matrix seek the maximum-weight independent set of the given graph, with weights given by the vector .[1][42]
For a matrix defined in this way from a perfect graph, the set of vectors satisfying the system of inequalities , form an integral polytope. It is the convex hull of the indicator vectors of independent sets in the graph, with facets corresponding to the maximal cliques in the graph. The perfect graphs are the only graphs for which the two polytopes defined in this way from independent sets and from maximal cliques coincide.[42]
Algorithms
In all perfect graphs, the graph coloring problem, maximum clique problem, and maximum independent set problem can all be solved in polynomial time. The algorithm for the general case involves the Lovász number of these graphs, which (for the complement of a given graph) is sandwiched between the chromatic number and clique number. Because these two numbers are equal for perfect graphs, they also both equal the Lovász number, and can be calculated by calculating the Lovász number. Calculating the Lovász number can be formulated as a semidefinite program and approximated numerically in polynomial time using the ellipsoid method for linear programming. For perfect graphs, rounding this approximation to an integer gives the chromatic number and clique number in polynomial time. The maximum clique itself, and an optimal coloring of the graph, can also be found by these methods, and a maximum independent set can be found by applying the same approach to the complement of the graph. However, solving these problems using the Lovász number and the ellipsoid method is complicated and has a high polynomial exponent.[43][44] More efficient combinatorial algorithms are known for many special cases.[45]
For many years the complexity of recognizing Berge graphs and perfect graphs remained open. From the definition of Berge graphs, it follows immediately that their recognition is in co-NP.[46] Finally, subsequent to the proof of the strong perfect graph theorem, a polynomial time algorithm was discovered by Chudnovsky, Cornuéjols, Liu, Seymour, and Vušković.[47]
Related concepts
Generalizing the perfect graphs, a graph class is said to be χ-bounded if the chromatic number of the graphs in the class can be bounded by a function of their clique number. The perfect graphs are exactly the graphs for which this function is the identity.[48]
The equality of the clique number and chromatic number in perfect graphs has motivated the definition of other graph classes, in which other graph invariants are set equal to each other. For instance, the domination perfect graphs are defined as graphs in which, in every induced subgraph, the smallest dominating set (a set of vertices adjacent to all remaining vertices) equals the size of the smallest independent set that is a dominating set. These include, for instance, the claw-free graphs.[49]
References
- Chudnovsky, Maria; Robertson, Neil; Seymour, Paul; Thomas, Robin (2003). "Progress on perfect graphs" (PDF). Mathematical Programming. 97 (1-2(B)): 405–422. doi:10.1007/s10107-003-0449-8. MR 2004404. Zbl 1028.05035.
- Lovász, László (1972). "Normal hypergraphs and the perfect graph conjecture". Discrete Mathematics. 2 (3): 253–267. doi:10.1016/0012-365X(72)90006-4. MR 0302480. Zbl 0239.05111.
- Chudnovsky, Maria; Robertson, Neil; Seymour, Paul; Thomas, Robin (2006). "The strong perfect graph theorem". Annals of Mathematics. 164 (1): 51–229. arXiv:math/0212070. doi:10.4007/annals.2006.164.51. MR 2233847. S2CID 119151552. Zbl 1112.05042.
- Lovász, László (1972). "A characterization of perfect graphs". Journal of Combinatorial Theory. Series B. 13 (2): 95–98. doi:10.1016/0095-8956(72)90045-7. MR 0309780. Zbl 0241.05107.
- Gallai, Tibor (1958). "Maximum-minimum Sätze über Graphen". Acta Mathematica Academiae Scientiarum Hungaricae. 9 (3–4): 395–434. doi:10.1007/BF02020271. MR 0124238. S2CID 123953062. Zbl 0084.19603.
- Berge, Claude (1961). "Färbung von Graphen deren sämtliche bzw. deren ungerade Kreise starr sind". Wiss. Z. Martin-Luther-Univ. Halle-Wittenberg Math.-Natur. Reihe. 10: 114.
- Berge, Claude (1963). "Perfect graphs". Six Papers on Graph Theory. Calcutta: Indian Statistical Institute. pp. 1–21.
- Chudnovsky et al. (2003); note that Chudnovsky et al define capacity using the complement of the graphs used for the definition in Shannon capacity of a graph, and include a logarithm that the linked article does not include.
- Hougardy, Stefan (2006). "Classes of perfect graphs". Discrete Mathematics. 306 (19–20): 2529–2571. doi:10.1016/j.disc.2006.05.021. MR 2261918. Zbl 1104.05029.
- "The 1991 D. R. Fulkerson Prizes in Discrete Mathematics" (PDF). 1991 Prize Recipients. Optima: Mathematical Optimization Society Newsletter (35): 4–8. November 1991. Retrieved 2023-01-21.
- Mackenzie, Dana (July 5, 2002). "Mathematics: Graph theory uncovers the roots of perfection". Science. 297 (5578): 38. doi:10.1126/science.297.5578.38. PMID 12098683.
- "2009 Fulkerson Prize Citation". Mathematical Optimization Society. Retrieved 2023-01-21.
- Chudnovsky, Maria; Seymour, Paul (2005). "The structure of claw-free graphs" (PDF). Surveys in combinatorics 2005. Papers from the 20th British combinatorial conference, University of Durham, Durham, UK, July 10–15, 2005. Cambridge University Press. pp. 153–171. ISBN 0-521-61523-2. MR 2187738. Zbl 1109.05092.
- "Bipartite graphs". Information System on Graph Classes and their Inclusions. Retrieved 2023-01-24.
- Kőnig, Dénes (1931). "Gráfok és mátrixok". Matematikai és Fizikai Lapok. 38: 116–119.
- Trotter, L. E., Jr. (1977). "Line perfect graphs". Mathematical Programming. 12 (2): 255–259. doi:10.1007/BF01593791. MR 0457293. Zbl 0366.05043.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Boros, E.; Gurvich, V. (2006). "Perfect graphs, kernels, and cores of cooperative games". Discrete Mathematics. 306 (19–20): 2336–2354. doi:10.1016/j.disc.2005.12.031. MR 2261906. Zbl 1103.05034.
- Kőnig, Dénes (1916). "Über Graphen und ihre Anwendung auf Determinantentheorie und Mengenlehre". Mathematische Annalen. 77: 453–465. doi:10.1007/BF01456961. JFM 46.0146.03. MR 1511872.
- Cornuéjols, Gérard (2002). "The strong perfect graph conjecture". Proceedings of the International Congress of Mathematicians, Vol. III (Beijing, 2002). Beijing: Higher Education Press. pp. 547–559. arXiv:math/0304464. MR 1957560. Zbl 1004.05034.
- Harzheim, Egbert (2005). "Comparability graphs". Ordered Sets. Advances in Mathematics. Vol. 7. New York: Springer. pp. 353–368. doi:10.1007/0-387-24222-8_12. ISBN 0-387-24219-8. MR 2127991. Zbl 1072.06001.
- Berge, Claude (1967). "Some classes of perfect graphs". Graph Theory and Theoretical Physics. London: Academic Press. pp. 155–165. MR 0232694. Zbl 0203.26403.
- Mirsky, Leon (1971). "A dual of Dilworth's decomposition theorem". The American Mathematical Monthly. 78 (8): 876–877. doi:10.2307/2316481. JSTOR 2316481. MR 0288054. Zbl 0263.06002.
- Perfect, Hazel (1980). "Remarks on Dilworth's theorem in relation to transversal theory". Glasgow Mathematical Journal. 21 (1): 19–22. doi:10.1017/S0017089500003931. MR 0558270. Zbl 0428.06001.
- Pnueli, A.; Lempel, A.; Even, S. (1971). "Transitive orientation of graphs and identification of permutation graphs". Canadian Journal of Mathematics. 23: 160–175. doi:10.4153/CJM-1971-016-5. MR 0292717. Zbl 0204.24604.
- Kolen, Antoon W. J.; Lenstra, Jan Karel; Papadimitriou, Christos H.; Spieksma, Frits C. R. (2007). "Interval scheduling: a survey". Naval Research Logistics. 54 (5): 530–543. doi:10.1002/nav.20231. MR 2335544. Zbl 1143.90337.
- Dagan, Ido; Golumbic, Martin Charles; Pinter, Ron Yair (1988). "Trapezoid graphs and their coloring". Discrete Applied Mathematics. 21 (1): 35–46. doi:10.1016/0166-218X(88)90032-7. MR 0953414. Zbl 0658.05067.
- Roberts, Fred S. (1969). "Indifference graphs". Proof Techniques in Graph Theory (Proc. Second Ann Arbor Graph Theory Conf., Ann Arbor, Mich., 1968). New York: Academic Press. pp. 139–146. MR 0252267. Zbl 0193.24205.
- Skrien, Dale J. (1982). "A relationship between triangulated graphs, comparability graphs, proper interval graphs, proper circular-arc graphs, and nested interval graphs". Journal of Graph Theory. 6 (3): 309–316. doi:10.1002/jgt.3190060307. MR 0666799. Zbl 0495.05027.
- Golumbic, Martin Charles (1978). "Trivially perfect graphs". Discrete Mathematics. 24 (1): 105–107. doi:10.1016/0012-365X(78)90178-4. MR 0522739. Zbl 0384.05057.
- Prömel, Hans Jürgen; Steger, Angelika (1992). "Almost all Berge graphs are perfect". Combinatorics, Probability and Computing. 1 (1): 53–79. doi:10.1017/S0963548300000079. MR 1167295. Zbl 0793.05063.
- McDiarmid, Colin; Yolov, Nikola (2019). "Random perfect graphs". Random Structures & Algorithms. 54 (1): 148–186. arXiv:1604.00890. doi:10.1002/rsa.20770. MR 3884617. Zbl 1405.05165.
- Bandelt, Hans-Jürgen; Mulder, Henry Martyn (1986). "Distance-hereditary graphs". Journal of Combinatorial Theory. Series B. 41 (2): 182–208. doi:10.1016/0095-8956(86)90043-2. MR 0859310. Zbl 0605.05024.
- Jung, H. A. (1978). "On a class of posets and the corresponding comparability graphs". Journal of Combinatorial Theory, Series B. 24 (2): 125–133. doi:10.1016/0095-8956(78)90013-8. Zbl 0382.05045.
- Corneil, D. G.; Lerchs, H.; Stewart Burlingham, L. (1981). "Complement reducible graphs". Discrete Applied Mathematics. 3 (3): 163–174. doi:10.1016/0166-218X(81)90013-5. MR 0619603. Zbl 0463.05057.
- Kay, David C.; Chartrand, Gary (1965). "A characterization of certain ptolemaic graphs". Canadian Journal of Mathematics. 17: 342–346. doi:10.4153/CJM-1965-034-0. MR 0175113. Zbl 0139.17301.
- Heggernes, Pinar; Kratsch, Dieter (2007). "Linear-time certifying recognition algorithms and forbidden induced subgraphs" (PDF). Nordic Journal of Computing. 14 (1–2): 87–108 (2008). MR 2460558. Zbl 1169.68653.
- "Threshold graphs". Information System on Graph Classes and their Inclusions. Retrieved 2023-02-12.
- Hoàng, C. T. (1987). "On a conjecture of Meyniel". Journal of Combinatorial Theory. Series B. 42 (3): 302–312. doi:10.1016/0095-8956(87)90047-5. MR 0888682. Zbl 0634.05058.
- Cicerone, Serafino; Di Stefano, Gabriele (1999). "Graph classes between parity and distance-hereditary graphs". Discrete Applied Mathematics. 95 (1–3): 197–216. doi:10.1016/S0166-218X(99)00075-X. MR 1708837. Zbl 0933.05144.
- Jansen, Klaus (1998). "A new characterization for parity graphs and a coloring problem with costs". In Lucchesi, Claudio L.; Moura, Arnaldo V. (eds.). LATIN '98: Theoretical Informatics, Third Latin American Symposium, Campinas, Brazil, April, 20-24, 1998, Proceedings. Lecture Notes in Computer Science. Vol. 1380. Springer. pp. 249–260. doi:10.1007/BFb0054326. hdl:11858/00-001M-0000-0014-7BE2-3. MR 1635464. Zbl 0910.05028.
- Golumbic, Martin Charles; Trenk, Ann N. (2004). Tolerance graphs. Cambridge Studies in Advanced Mathematics. Vol. 89. Cambridge University Press. doi:10.1017/CBO9780511542985. ISBN 0-521-82758-2. MR 2051713.
- Chvátal, Václav (1975). "On certain polytopes associated with graphs". Journal of Combinatorial Theory, Series B. 18: 138–154. doi:10.1016/0095-8956(75)90041-6. MR 0371732. Zbl 0277.05139.
- Grötschel, Martin; Lovász, László; Schrijver, Alexander (1984). "Polynomial algorithms for perfect graphs". In Berge, C.; Chvátal, V. (eds.). Topics on perfect graphs. North-Holland Mathematics Studies. Vol. 88. North-Holland, Amsterdam. pp. 325–356. doi:10.1016/S0304-0208(08)72943-8. MR 0778770.
- Grötschel, Martin; Lovász, László; Schrijver, Alexander (1988). Geometric Algorithms and Combinatorial Optimization. Springer-Verlag. MR 0936633. Zbl 0634.05001. See especially chapter 9, "Stable Sets in Graphs", pp. 273–303.
- Golumbic, Martin Charles (1980). Algorithmic Graph Theory and Perfect Graphs. Academic Press. doi:10.1016/C2013-0-10739-8. ISBN 0-444-51530-5. Second edition, Annals of Discrete Mathematics 57, Elsevier, 2004.
- Lovász, László (1983). "Perfect graphs". In Beineke, Lowell W.; Wilson, Robin J. (eds.). Selected Topics in Graph Theory, Vol. 2. Academic Press. pp. 55–87. ISBN 0-12-086202-6.
- Chudnovsky, Maria; Cornuéjols, Gérard; Liu, Xinming; Seymour, Paul; Vušković, Kristina (2005). "Recognizing Berge graphs". Combinatorica. 25 (2): 143–186. doi:10.1007/s00493-005-0012-8.
- Gyárfás, A. (1987). "Problems from the world surrounding perfect graphs" (PDF). Proceedings of the International Conference on Combinatorial Analysis and its Applications (Pokrzywna, 1985). Zastosowania Matematyki. 19 (3–4): 413–441 (1988). MR 0951359.
- Faudree, Ralph; Flandrin, Evelyne; Ryjáček, Zdeněk (1997). "Claw-free graphs — A survey". Discrete Mathematics. 164 (1–3): 87–147. doi:10.1016/S0012-365X(96)00045-3. MR 1432221.
External links
- The Strong Perfect Graph Theorem by Václav Chvátal.
- Open problems on perfect graphs, maintained by the American Institute of Mathematics.
- Perfect Problems, maintained by Václav Chvátal.
- Information System on Graph Class Inclusions: perfect graph