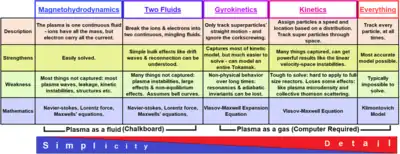
Plasma modeling
Plasma modeling refers to solving equations of motion that describe the state of a plasma. It is generally coupled with Maxwell's equations for electromagnetic fields or Poisson's equation for electrostatic fields. There are several main types of plasma models: single particle, kinetic, fluid, hybrid kinetic/fluid, gyrokinetic and as system of many particles.
Single particle description
The single particle model describes the plasma as individual electrons and ions moving in imposed (rather than self-consistent) electric and magnetic fields. The motion of each particle is thus described by the Lorentz Force Law. In many cases of practical interest, this motion can be treated as the superposition of a relatively fast circular motion around a point called the guiding center and a relatively slow drift of this point.
Kinetic description
The kinetic model is the most fundamental way to describe a plasma, resultantly producing a distribution function
where the independent variables and are position and velocity, respectively. A kinetic description is achieved by solving the Boltzmann equation or, when the correct description of long-range Coulomb interaction is necessary, by the Vlasov equation which contains self-consistent collective electromagnetic field, or by the Fokker–Planck equation, in which approximations have been used to derive manageable collision terms. The charges and currents produced by the distribution functions self-consistently determine the electromagnetic fields via Maxwell's equations.
Fluid description
To reduce the complexities in the kinetic description, the fluid model describes the plasma based on macroscopic quantities (velocity moments of the distribution such as density, mean velocity, and mean energy). The equations for macroscopic quantities, called fluid equations, are obtained by taking velocity moments of the Boltzmann equation or the Vlasov equation. The fluid equations are not closed without the determination of transport coefficients such as mobility, diffusion coefficient, averaged collision frequencies, and so on. To determine the transport coefficients, the velocity distribution function must be assumed/chosen. But this assumption can lead to a failure of capturing some physics.
Hybrid kinetic/fluid description
Although the kinetic model describes the physics accurately, it is more complex (and in the case of numerical simulations, more computationally intensive) than the fluid model. The hybrid model is a combination of fluid and kinetic models, treating some components of the system as a fluid, and others kinetically. The hybrid model is sometimes applied in space physics, when the simulation domain exceeds thousands of ion gyroradius scales, making it impractical to solve kinetic equations for electrons. In this approach, magnetohydrodynamic fluid equations describe electrons, while the kinetic Vlasov equation describes ions. [1] [2]
Gyrokinetic description
In the gyrokinetic model, which is appropriate to systems with a strong background magnetic field, the kinetic equations are averaged over the fast circular motion of the gyroradius. This model has been used extensively for simulation of tokamak plasma instabilities (for example, the GYRO and Gyrokinetic ElectroMagnetic codes), and more recently in astrophysical applications.
Quantum mechanical methods
Quantum methods are not yet very common in plasma modeling. They can be used to solve unique modeling problems; like situations where other methods do not apply.[3] They involve the application of quantum field theory to plasma. In these cases, the electric and magnetic fields made by particles are modeled like a field; A web of forces. Particles that move, or are removed from the population push and pull on this web of forces, this field. The mathematical treatment for this involves Lagrangian mathematics.
Commercial plasma physics modeling codes
See also
References
- Pokhotelov, D.; von Alfthan, S.; Kempf, Y.; Vainio, R.; Koskinen, H.E.J.; Palmroth, M. (2013). "Ion distributions upstream and downstream of the Earth's bow shock: First results from Vlasiator". Ann. Geophys. 31 (12): 2207–2212. doi:10.5194/angeo-31-2207-2013. hdl:10138/161497.
- von Alfthan, S.; Pokhotelov, D.; Kempf, Y.; Hoilijoki, S.; Honkonen, I.; Sandroos, A.; Palmroth, M. (2014). "Vlasiator: First global hybrid-Vlasov simulations of Earth's foreshock and magnetosheath". J. Atmos. Sol. Terr. Phys. 120: 24–35. doi:10.1016/j.jastp.2014.08.012.
- Hedditch, John (2018). "A different approach to the MHD equilibrium". arXiv:1808.00622 [physics.plasm-ph].
- Francis F. Chen (2006). Introduction to Plasma Physics and Controlled Fusion (2nd ed.). Springer. ISBN 978-0-306-41332-2.
- Nicholas Krall & Alvin Trivelpiece (1986). Principles of Plasma Physics. San Francisco Press. ISBN 978-0-911302-58-5.
- Ledvina, S. A.; Y.-J. Ma; E. Kallio (2008). "Modeling and Simulating Flowing Plasmas and Related Phenomena". Space Science Reviews. 139 (1–4): 143. Bibcode:2008SSRv..139..143L. doi:10.1007/s11214-008-9384-6. S2CID 121999061.