Poisson wavelet
In mathematics, in functional analysis, several different wavelets are known by the name Poisson wavelet. In one context, the term "Poisson wavelet" is used to denote a family of wavelets labeled by the set of positive integers, the members of which are associated with the Poisson probability distribution. These wavelets were first defined and studied by Karlene A. Kosanovich, Allan R. Moser and Michael J. Piovoso in 1995–96.[1][2] In another context, the term refers to a certain wavelet which involves a form of the Poisson integral kernel.[3] In still another context, the terminology is used to describe a family of complex wavelets indexed by positive integers which are connected with the derivatives of the Poisson integral kernel.[4]
Wavelets associated with Poisson probability distribution
Definition
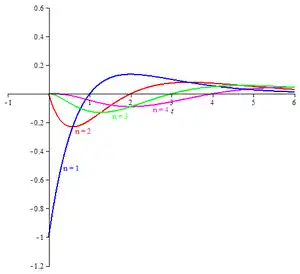
For each positive integer n the Poisson wavelet is defined by
To see the relation between the Poisson wavelet and the Poisson distribution let X be a discrete random variable having the Poisson distribution with parameter (mean) t and, for each non-negative integer n, let Prob(X = n) = pn(t). Then we have
The Poisson wavelet is now given by
Basic properties
- is the backward difference of the values of the Poisson distribution:
- The "waviness" of the members of this wavelet family follows from
- The Fourier transform of is given
- The admissibility constant associated with is
- Poisson wavelet is not an orthogonal family of wavelets.
Poisson wavelet transform
The Poisson wavelet family can be used to construct the family of Poisson wavelet transforms of functions defined the time domain. Since the Poisson wavelets satisfy the admissibility condition also, functions in the time domain can be reconstructed from their Poisson wavelet transforms using the formula for inverse continuous-time wavelet transforms.
If f(t) is a function in the time domain its n-th Poisson wavelet transform is given by
In the reverse direction, given the n-th Poisson wavelet transform of a function f(t) in the time domain, the function f(t) can be reconstructed as follows:
Applications
Poisson wavelet transforms have been applied in multi-resolution analysis, system identification, and parameter estimation. They are particularly useful in studying problems in which the functions in the time domain consist of linear combinations of decaying exponentials with time delay.
Wavelet associated with Poisson kernel
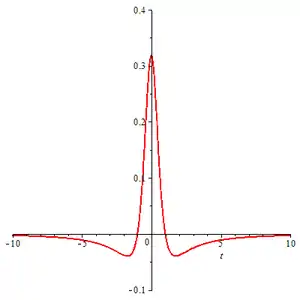
Definition
The Poisson wavelet is defined by the function[3]
This can be expressed in the form
- where .
Relation with Poisson kernel
The function appears as an integral kernel in the solution of a certain initial value problem of the Laplace operator.
This is the initial value problem: Given any in , find a harmonic function defined in the upper half-plane satisfying the following conditions:
- , and
- as in .
The problem has the following solution: There is exactly one function satisfying the two conditions and it is given by
where and where "" denotes the convolution operation. The function is the integral kernel for the function . The function is the harmonic continuation of into the upper half plane.
Properties
- The "waviness" of the function follows from
- .
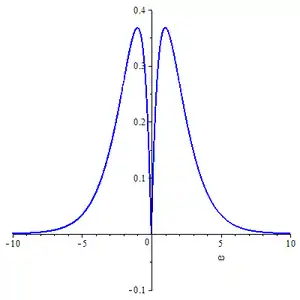
- The Fourier transform of is given by
- .
- The admissibility constant is
A class of complex wavelets associated with the Poisson kernel
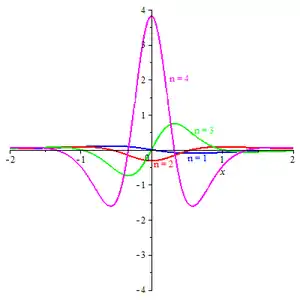
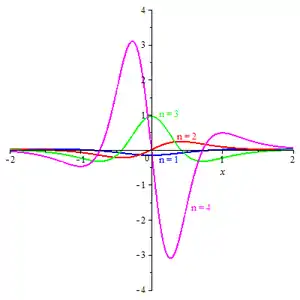
Definition
The Poisson wavelet is a family of complex valued functions indexed by the set of positive integers and defined by[4][5]
- where
Relation with Poisson kernel
The function can be expressed as an n-th derivative as follows:
Writing the function in terms of the Poisson integral kernel as
we have
Thus can be interpreted as a function proportional to the derivatives of the Poisson integral kernel.
References
- Karlene A. Kosanovich, Allan R. Moser and Michael J. Piovoso (1996). "The Poisson wavelet transform". Chemical Engineering Communications. 146 (1): 131–138. doi:10.1080/00986449608936485.
- Karlene A. Kosanovich, Allan R. Moser and Michael J. Piovoso (1997). "A new family of wavelets: the Poisson wavelet transform". Computers in Chemical Engineering. 21 (6): 601–620. doi:10.1016/S0098-1354(96)00294-3.
- Roland Klees, Roger Haagmans (editors) (2000). Wavelets in the Geosciences. Berlin: Springer. pp. 18–20.
{{cite book}}:|last1=has generic name (help) - Abdul J. Jerri (1998). The Gibbs Phenomenon in Fourier Analysis, Splines and Wavelet Approximations. Dordrech: Springer Science+Business Media. pp. 222–224. ISBN 978-1-4419-4800-7.
- Wojbor A. Woyczynski (1997). Distributions in the Physical and Engineering Sciences: Distributional and Fractal Calculus, Integral Transforms and Wavelets, Volume 1. Springer Science & Business Media. p. 223. ISBN 9780817639242.