Polygon with holes
In geometry, a polygon with holes is an area-connected planar polygon with one external boundary and one or more interior boundaries (holes).[1] Polygons with holes can be dissected into multiple polygons by adding new edges, so they are not frequently needed.
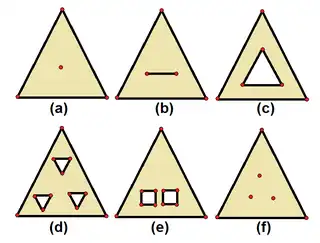 Polygons with holes, with simply connected brown regions and interior boundaries, including degenerate cases of single vertices and edges, (a,b,f). | |
 Circular |
 Pentagonal |
| An annulus can be approximated by two n-sided boundaries with the same center, but different radius. | |
An ordinary polygon can be called simply-connected, while a polygon-with-holes is multiply-connected. An H-holed-polygon is H-connected.[2]
Degenerate holes
Degenerate cases may be considered, but a well-formed holed-polygon must have no contact between exterior and interior boundaries, or between interior boundaries. Nondegenerate holes should have 3 or more sides, excluding internal point boundaries (monogons) and single edge boundaries (digons).
Boundary orientation
Area fill algorithms in computational lists the external boundary vertices can be listed in counter-clockwise order, and interior boundaries clockwise. This allows the interior area to be defined as left of each edge.[3]
Conversion to ordinary polygon
A polygons with holes can be transformed into an ordinary unicursal boundary path by adding (degenerate) connecting double-edges between boundaries, or by dissecting or triangulating it into 2 or more simple polygons.
 Example conversion of a single-holed polygon by connecting edges, or dissection
Example conversion of a single-holed polygon by connecting edges, or dissection
In polyhedra
Polygons with holes can be seen as faces in polyhedra, like a cube with a smaller cube externally placed on one of its square faces (augmented), with their common surfaces removed. A toroidal polyhedron can also be defined connecting a holed-face to a holed-faced on the opposite side (excavated). The 1-skeleton (vertices and edges) of a polyhedron with holed-faces is not a connected graph. Each set of connected edges will make a separate polyhedron if their edge-connected holes are replaced with faces.
The Euler characteristic of hole-faced polyhedron is χ = V - E + F = 2(1-g) + H, genus g, for V vertices, E edges, F faces, and H holes in the faces.
- Examples
 (genus 0) with two 1-holed-faces (top and bottom).
(genus 0) with two 1-holed-faces (top and bottom).
V=16, E=20, F=8, H=2.
3-connected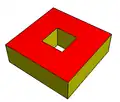 Toroid (genus 1) with two 1-holed-faces.
Toroid (genus 1) with two 1-holed-faces.
V=16, E=24, F=10, H=2.
2-connected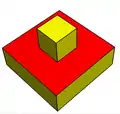 (genus 0) with one 1-holed-face.
(genus 0) with one 1-holed-face.
V=16, E=24, F=11, H=1.
2-connected (genus 0), with six 1-holed faces.
(genus 0), with six 1-holed faces.
V=32, E=36, F=12, H=6.
7-connected Toroid (genus 5), with six 1-holed faces.
Toroid (genus 5), with six 1-holed faces.
V=40, E=72, F=30, H=6.
2-connected Toroid (genus 2) with two 2-holed-faces.
Toroid (genus 2) with two 2-holed-faces.
V=24, E=36, F=14, H=4.
3-connected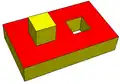 Toroid (genus 1) with one 2-holed-face, and one 1-holed-face.
Toroid (genus 1) with one 2-holed-face, and one 1-holed-face.
V=24, E=36, F=15, H=3.
3-connected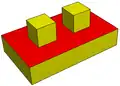 (genus 0) with one 2-holed-face.
(genus 0) with one 2-holed-face.
V=24, E=36, F=16, H=2.
3-connected Toroid (genus 1) with two 1-holed-faces.
Toroid (genus 1) with two 1-holed-faces.
V=24, E=36, F=14, H=2.
2-connected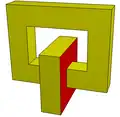 Toroid (genus 1) with two 1-holed-faces.
Toroid (genus 1) with two 1-holed-faces.
V=32, E=48, F=18, H=2.
2-connected
- Examples with degenerate holes
A face with a point hole is considered a monogonal hole, adding one vertex, and one edge, and can attached to a degenerate monogonal hosohedron hole, like a cylinder hole with zero radius. A face with a degenerate digon hole adds 2 vertices and 2 coinciding edges, where the two edges attach to two coplanar faces, as a dihedron hole.
References
- The Geometry of n Dimensions, D. M. Y. Summerville, p.144 Ring-shaped polygons
- http://www.science.smith.edu/~jorourke/books/ArtGalleryTheorems/Art_Gallery_Chapter_5.pdf
- Jorge Urrutia, in Handbook of Computational Geometry, 2000

