Polygonalization

A polygonalization is a simple polygon having a given set of points in the Euclidean plane as its set of vertices. A polygon may be described by a cyclic order on its vertices, which are connected in consecutive pairs by line segments, the edges of the polygon. A polygon, defined in this way, is "simple" if the only intersection points of these line segments are at shared endpoints.[2]

Some authors only consider polygonalizations for points that are in general position, meaning that no three are on a line.[7] With this assumption, the angle between two consecutive segments of the polygon cannot be 180°. However, when point sets with collinearities are considered, it is generally allowed for their polygonalizations to have 180° angles at some points. When this happens, these points are still considered to be vertices, rather than being interior to edges.[8]

Polygonalizations of a 3 × 3 grid. The 180° angles visible in each polygon are necessary: for a grid of this size, all polygonalizations have a 180° angle.[9]

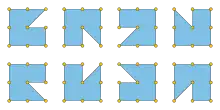
Steinhaus (1964) observed that every finite point set with no three in a line forms the vertices of a simple polygon.[10] However, requiring no three to be in a line is unnecessarily strong. Instead, all that is required for the existence of a polygonalization (allowing 180° angles) is that the points do not all lie on one line. If they do not, then they have a polygonalization that can be constructed in polynomial time. One way of constructing a polygonalization is to choose any point ${\displaystyle q}$ in the convex hull of ${\displaystyle P}$ (not necessarily one of the given points). Then radially ordering the points around ${\displaystyle q}$ (breaking ties by distance from q) produces the cyclic ordering of a star-shaped polygon through all the given points, with ${\displaystyle q}$ in its kernel.[7] The same idea of sorting points radially around a central point is used in some versions of the Graham scan convex hull algorithm, and can be performed in ${\displaystyle O(n\log n)}$ time.[11] Polygonalizations that avoid 180° angles do not always exist. For instance, for 3 × 3 and 5 × 5 square grids, all polygonalizations use 180° angles.[9]

As well as star-shaped polygonalizations, every non-collinear set of points has a polygonalization that is a monotone polygon. This means that, with respect to some straight line (which may be taken as the ${\displaystyle x}$-axis) every perpendicular line to the reference line intersects the polygon in a single interval, or not at all. A construction of Grünbaum (1994) begins by sorting the points by their ${\displaystyle x}$-coordinates, and drawing a line through the two extreme points. Because the points are not all in a line, at least one of the two open halfplanes bounded by this line must be non-empty. Grünbaum forms two monotone polygonal chains connecting the extreme points through sorted subsequences of the points: one for the points in this non-empty open halfplane, and the other for the remaining points. Their union is the desired monotone polygon. After the sorting step, the rest of the construction may be performed in linear time.[4]

It is NP-complete to determine whether a set of points has a polygonalization using only axis-parallel edges.[12] However, polygonalizations with the additional constraint that they make a right turn at every vertex, if they exist, are uniquely determined. Each axis-parallel line through a point must pass through an even number of points, and this polygonalization must connect alternating pairs of points on this line. The polygonalization may be found in time ${\displaystyle O(n\log n)}$ by grouping the points by equal coordinates and sorting each group by the other coordinate.[13] For any point set, at most one rotation can have a polygonalization of this form, and this rotation can again be found in polynomial time.[14]

Problems of finding an optimal polygonalization (for various criteria of optimality) are often computationally infeasible. For instance, the solution to the travelling salesman problem, for the given points, does not have any crossings. Therefore, it is always a polygonalization, the polygonalization with the minimum perimeter.[15] It is NP-hard to find. Similarly, finding the simple polygonalization with minimum or maximum area is known to be NP-hard,[3] and has been the subject of some computational efforts.[16][17] The maximum area is always more than half of the area of the convex hull, giving an approximation ratio of 2.[18] The exact complexity of the simple polygonalization with maximum perimeter, and the existence of a constant approximation ratio for this problem, remain unknown.[5] The polygonalization that minimizes the length of its longest edge is also NP-hard to find, and hard to approximate to an approximation ratio better than ${\displaystyle {\sqrt {3}}}$; no constant-factor approximation is known.[19]

A non-optimal solution to the travelling salesman problem may have crossings, but it is possible to eliminate all crossings by local optimization steps that reduce the total length. Using steps that also eliminate crossings at each step, this can be done in polynomial time,[20] but without this restriction there exist local optimization sequences that instead use an exponential number of steps.[21]

The shortest bitonic tour (the minimum-perimeter monotone polygon through the given points) is always a polygonalization, and can be found in polynomial time.[22]

The problem of counting all polygonalizations of a given point set belongs to #P, the class of counting problems associated with decision problems in NP. However, it is unknown whether it is #P-complete or, if not, what its computational complexity might be.[23][24] A set of points has exactly one polygonalization if and only if it is in convex position.[1] There exist sets of ${\displaystyle n}$ points for which the number of polygonalizations is as large as ${\displaystyle 4.64^{n}}$,[25] and every set of ${\displaystyle n}$ points has at most ${\displaystyle 54.6^{n}}$ polygonalizations.[6]

Methods applying the planar separator theorem to labeled triangulations of the points can be used to count all polygonalizations of a set of ${\displaystyle n}$ points in subexponential time, ${\displaystyle n^{O({\sqrt {n}})}}$.[26] Dynamic programming can be used to count all monotone polygonalizations in polynomial time, and the results of this computation can then be used to generate a random monotone polygonalization.[27]

A polygon that cannot be changed into any other polygon through the same points by flips or VE-flips[28]

It is unknown whether it is possible for the system of all polygonalizations to form a connected state space under local moves that change a bounded number of the edges of the polygonalizations. If this were possible, it could be used as part of an algorithm for generating all polygonalizations, by applying a graph traversal to the state space. For this problem, it is insufficient to consider flips that remove two edges of a polygonalization and replace them by two other edges, or VE-flips that remove three edges, two of which share a vertex, and replace them by three other edges. There exist polygonalizations for which no flip or VE-flip is possible, even though the same point set has other polygonalizations.[28]

The polygonal wraps, weakly simple polygons that use each given point one or more times as a vertex, include all polygonalizations and are connected by local moves.[2] Another more general class of polygons, the surrounding polygons, are simple polygons that have some of the given points as vertices and enclose all of the points. They are again locally connected, and can be listed in polynomial time per polygon. The algorithm constructs a tree of polygons, with the convex hull as its root and with the parent of each other surrounding polygon obtained by removing one vertex (proven to be possible by applying the two ears theorem to the exterior of the polygon). It then applies a reverse-search algorithm to this tree to list the polygons. As a consequence of this method, all polygonalizations can be listed in exponential time (${\displaystyle 2^{O(n)}}$ for ${\displaystyle n}$ points) and polynomial space.[29]

Classical connect the dots puzzles involve connecting points in sequence to form some unexpected shape, often without crossings.[30] The travelling salesman problem and its variants have many applications.[31] Polygonalization also has applications in the reconstruction of contour lines from scattered data points, and in boundary tracing in image analysis.[32]

• Denjoy–Riesz theorem, on sets of infinitely many points that can be connected by a Jordan arc