Poncelet point
In geometry, the Poncelet point of four given points is defined as follows:
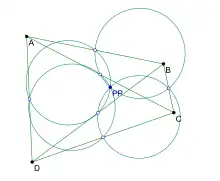
Let A, B, C, D be four points in the plane that do not form an orthocentric system and such that no three of them are collinear. The nine-point circles of triangles △ABC, △BCD, △CDA, △DAB meet at one point, the Poncelet point of the points A, B, C, D. (If A, B, C, D do form an orthocentric system, then triangles △ABC, △BCD, △CDA, △DAB all share the same nine-point circle, and the Poncelet point is undefined.)
Properties
If A, B, C, D do not lie on a circle, the Poncelet point of A, B, C, D lies on the circumcircle of the pedal triangle of D with respect to triangle △ABC and lies on the other analogous circles. (If they do lie on a circle, then those pedal triangles will be lines; namely, the Simson line of D with respect to triangle △ABC, and the other analogous Simson lines. In that case, those lines still concur at the Poncelet point, which will also be the anticenter of the cyclic quadrilateral whose vertices are A, B, C, D.)
The Poncelet point of A, B, C, D lies on the circle through the intersection of lines AB and CD, the intersection of lines AC and BD, and the intersection of lines AD and BC (assuming all these intersections exist).
The Poncelet point of A, B, C, D is the center of the unique rectangular hyperbola through A, B, C, D.
References
- Vonk, Jan (2009), "The Feuerbach point and reflections of the Euler line" (PDF), Forum Geometricorum, 9: 47–55
- Poncelet points and antigonal conjugates