Post-Minkowskian expansion

In physics, precisely in the general theory of relativity, post-Minkowskian expansions (PM) or post-Minkowskian approximations are mathematical methods used to find approximate solutions of Einstein's equations by means of a power series development of the metric tensor.

Post-minkowskian vs Post-newtonian expansions

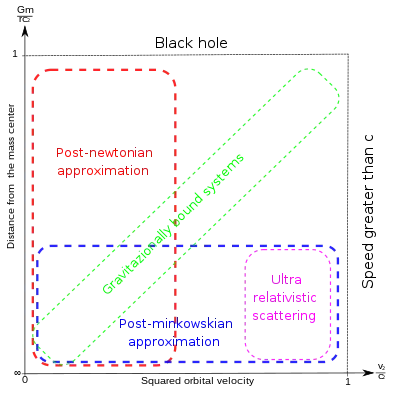
Unlike post-Newtonian expansions (PN), in which the series development is based on a combination of powers of the velocity (which must be negligible compared to that of light) and the gravitational constant, in the post-Minkowskian case the developments are based only on the gravitational constant, allowing analysis even at velocities close to that of light (relativistic).[1]

	0PN		1PN		2PN		3PN		4PN		5PN		6PN		7PN
1PM	( 1	+	${\displaystyle v^{2}}$	+	${\displaystyle v^{4}}$	+	${\displaystyle v^{6}}$	+	${\displaystyle v^{8}}$	+	${\displaystyle v^{10}}$	+	${\displaystyle v^{12}}$	+	${\displaystyle v^{14}}$	+	...)	${\displaystyle G^{1}}$
2PM			( 1	+	${\displaystyle v^{2}}$	+	${\displaystyle v^{4}}$	+	${\displaystyle v^{6}}$	+	${\displaystyle v^{8}}$	+	${\displaystyle v^{10}}$	+	${\displaystyle v^{12}}$	+	...)	${\displaystyle G^{2}}$
3PM					( 1	+	${\displaystyle v^{2}}$	+	${\displaystyle v^{4}}$	+	${\displaystyle v^{6}}$	+	${\displaystyle v^{8}}$	+	${\displaystyle v^{10}}$	+	...)	${\displaystyle G^{3}}$
4PM							( 1	+	${\displaystyle v^{2}}$	+	${\displaystyle v^{4}}$	+	${\displaystyle v^{6}}$	+	${\displaystyle v^{8}}$	+	...)	${\displaystyle G^{4}}$
5PM									( 1	+	${\displaystyle v^{2}}$	+	${\displaystyle v^{4}}$	+	${\displaystyle v^{6}}$	+	...)	${\displaystyle G^{5}}$
6PM											( 1	+	${\displaystyle v^{2}}$	+	${\displaystyle v^{4}}$	+	...)	${\displaystyle G^{6}}$
Comparison table of powers used for PN and PM approximations in the case of two non-rotating bodies. 0PN corresponds to the case of Newton's theory of gravitation. 0PM (not shown) corresponds to the Minkowsky flat space.[2]

One of the earliest works on this method of resolution is that of Bruno Bertotti, published in Nuovo Cimento in 1956.[3]