Prism graph

The individual graphs may be named after the associated solid:

• Triangular prism graph – 6 vertices, 9 edges
• Cubical graph – 8 vertices, 12 edges
• Pentagonal prism graph – 10 vertices, 15 edges
• Hexagonal prism graph – 12 vertices, 18 edges
• Heptagonal prism graph – 14 vertices, 21 edges
• Octagonal prism graph – 16 vertices, 24 edges
• ...

Y3 = GP(3,1)

Y4 = Q3 = GP(4,1)

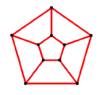Y5 = GP(5,1)

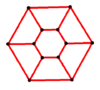Y6 = GP(6,1)

Y7 = GP(7,1)

Y8 = GP(8,1)

Although geometrically the star polygons also form the faces of a different sequence of (self-intersecting and non-convex) prismatic polyhedra, the graphs of these star prisms are isomorphic to the prism graphs, and do not form a separate sequence of graphs.

Prism graphs are examples of generalized Petersen graphs, with parameters GP(n,1). They may also be constructed as the Cartesian product of a cycle graph with a single edge.[1]

As with many vertex-transitive graphs, the prism graphs may also be constructed as Cayley graphs. The order-n dihedral group is the group of symmetries of a regular n-gon in the plane; it acts on the n-gon by rotations and reflections. It can be generated by two elements, a rotation by an angle of 2π/n and a single reflection, and its Cayley graph with this generating set is the prism graph. Abstractly, the group has the presentation ${\displaystyle \langle r,f\mid r^{n},f^{2},(rf)^{2}\rangle }$ (where r is a rotation and f is a reflection or flip) and the Cayley graph has r and f (or r, r⁻¹, and f) as its generators.[1]

The n-gonal prism graphs with odd values of n may be constructed as circulant graphs ${\displaystyle C_{2n}^{2,n}}$. However, this construction does not work for even values of n.[1]

The graph of an n-gonal prism has 2n vertices and 3n edges. They are regular, cubic graphs. Since the prism has symmetries taking each vertex to each other vertex, the prism graphs are vertex-transitive graphs. As polyhedral graphs, they are also 3-vertex-connected planar graphs. Every prism graph has a Hamiltonian cycle.[2]

Among all biconnected cubic graphs, the prism graphs have within a constant factor of the largest possible number of 1-factorizations. A 1-factorization is a partition of the edge set of the graph into three perfect matchings, or equivalently an edge coloring of the graph with three colors. Every biconnected n-vertex cubic graph has O(2^n/2) 1-factorizations, and the prism graphs have Ω(2^n/2) 1-factorizations.[3]

The number of spanning trees of an n-gonal prism graph is given by the formula[4]

${\displaystyle {\frac {n}{2}}{\bigl (}(2+{\sqrt {3}})^{n}+(2-{\sqrt {3}})^{n}-2){\bigr .}}$

For n = 3, 4, 5, ... these numbers are

75, 384, 1805, 8100, 35287, 150528, ... (sequence A006235 in the OEIS).

The n-gonal prism graphs for even values of n are partial cubes. They form one of the few known infinite families of cubic partial cubes, and (except for four sporadic examples) the only vertex-transitive cubic partial cubes.[5]

The pentagonal prism is one of the forbidden minors for the graphs of treewidth three.[6] The triangular prism and cube graph have treewidth exactly three, but all larger prism graphs have treewidth four.

Other infinite sequences of polyhedral graph formed in a similar way from polyhedra with regular-polygon bases include the antiprism graphs (graphs of antiprisms) and wheel graphs (graphs of pyramids). Other vertex-transitive polyhedral graphs include the Archimedean graphs.

If the two cycles of a prism graph are broken by the removal of a single edge in the same position in both cycles, the result is a ladder graph. If these two removed edges are replaced by two crossed edges, the result is a non-planar graph called a Möbius ladder.[7]