Quantum paraelectricity

Quantum paraelectricity[1] is a type of incipient ferroelectricity where the onset of ferroelectric order is suppressed by quantum fluctuations.[2] From the soft mode theory of ferroelectricity,[3] this occurs when a ferroelectric instability is stabilized by quantum fluctuations. In this case the soft-mode frequency never becomes unstable (Fig. 1a) as opposed to a regular ferroelectric.

a) Ferroelectric soft-mode frequency as a function of temperature. The dashed lines shows the behaviour of a regular ferroelectric material with a ferroelectric instability at the Curie temperature. The solid lines shows the quantum paraelectric frequency with quantum fluctuations preventing a ferroelectric instability from arising. b) The dashed line shows the divergence of the dielectric susceptibility near the Curie temperature for a regular ferroelectric. The solid line indicates the anomalous behaviour of a quantum paraelectric where the dielectric susceptibility begins to diverge in the regular manner but levels off.

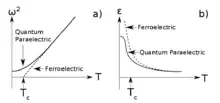
Experimentally this is associated with an anomalous behaviour of the dielectric susceptibility, for example in SrTiO₃.[4] In a normal ferroelectric, close to the onset of the phase transition the dielectric susceptibility diverges as the temperature approaches the Curie temperature. However, in the case of a quantum paraelectric the dielectric susceptibility diverges until it reaches a temperature low enough for quantum effects to cancel out the ferroelectricity (Fig. 1b). In the case of SrTiO₃ this is around 4K.

Other known quantum paraelectrics are KTaO₃ and potentially CaTiO₃.[5]