Quasi-delay-insensitive circuit
In digital logic design, an asynchronous circuit is quasi delay-insensitive (QDI) when it operates correctly, independent of gate and wire delay with the weakest exception necessary to be turing-complete.[timing 1][timing 2]
Overview
Pros
- Robust to process variation, temperature fluctuation, circuit redesign, and FPGA remapping.
- Natural event sequencing facilitates complex control circuitry.
- Automatic clock gating and compute-dependent cycle time can save dynamic power and increase throughput by optimizing for average-case workload characteristics instead of worst-case.
Cons
- Delay insensitive encodings generally require twice as many wires for the same data.
- Communication protocols and encodings generally require twice as many devices for the same functionality.
Chips
QDI circuits have been used to manufacture a large number of research chips, a small selection of which follows.
Theory
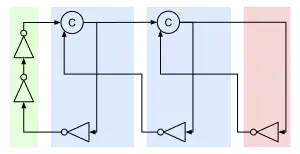
The simplest QDI circuit is a ring oscillator implemented using a cycle of inverters. Each gate drives two events on its output node. Either the pull up network drives node's voltage from GND to Vdd or the pull down network from VDD to GND. This gives the ring oscillator six events in total.
Multiple cycles may be connected using a multi-input gate. A c-element, which waits for its inputs to match before copying the value to its output, may be used to synchronize multiple cycles. If one cycle reaches the c-element before another, it is forced to wait. Synchronizing three or more of these cycles creates a pipeline allowing the cycles to trigger one after another.
If cycles are known to be mutually exclusive, then they may be connected using combinational logic (AND, OR). This allows the active cycle to continue regardless of the inactive cycles, and is generally used to implement delay insensitive encodings.
For larger systems, this is too much to manage. So, they are partitioned into processes. Each process describes the interaction between a set of cycles grouped into channels, and the process boundary breaks these cycles into channel ports. Each port has a set of request nodes that tend to encode data and acknowledge nodes that tend to be dataless. The process that drives the request is the sender while the process that drives the acknowledgement is the receiver. Now, the sender and receiver communicate using certain protocols[synthesis 1] and the sequential triggering of communication actions from one process to the next is modeled as a token traversing the pipeline.
Stability and non-interference
The correct operation of a QDI circuit requires that events be limited to monotonic digital transitions. Instability (glitch) or interference (short) can force the system into illegal states causing incorrect/unstable results, deadlock, and circuit damage. The previously described cyclic structure that ensures stability is called acknowledgement. A transition T1 acknowledges another T2 if there is a causal sequence of events from T1 to T2 that prevents T2 from occurring until T1 has completed.[timing 3][timing 4][timing 1] For a DI circuit, every transition must acknowledge every input to its associated gate. For a QDI circuit, there are a few exceptions in which the stability property is maintained using timing assumptions guaranteed with layout constraints rather than causality.[layout 1]
Isochronic fork assumption
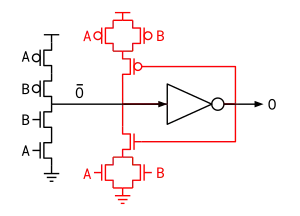
An isochronic fork is a wire fork in which one end does not acknowledge the transition driving the wire. A good example of such a fork can be found in the standard implementation of a pre-charge half buffer. There are two types of Isochronic forks. An asymmetric isochronic fork assumes that the transition on the non-acknowledging end happens before or when the transition has been observed on the acknowledging end. A symmetric isochronic fork ensures that both ends observe the transition simultaneously. In QDI circuits, every transition that drives a wire fork must be acknowledged by at least one end of that fork. This concept was first introduced by A. J. Martin to distinguish between asynchronous circuits that satisfy QDI requirements and those that do not. Martin also established that it is impossible to design useful systems without including at least some isochronic forks given reasonable assumptions about the available circuit elements.[timing 1] Isochronic forks were long thought to be the weakest compromise away from fully delay-insensitive systems.
In fact, every CMOS gate has one or more internal isochronic forks between the pull-up and pull-down networks. The pull-down network only acknowledges the up-going transitions of the inputs while the pull-up network only acknowledges the down-going transitions.
Adversarial path assumption
The adversarial path assumption also deals with wire forks, but is ultimately weaker than the isochronic fork assumption. At some point in the circuit after a wire fork, the two paths must merge back into one. The adversarial path is the one that fails to acknowledge the transition on the wire fork. This assumption states that the transition propagating down the acknowledging path reaches the merge point after it would have down the adversarial path.[timing 4] This effectively extends the isochronic fork assumption beyond the confines of the forked wire and into the connected paths of gates.
Half-cycle timing assumption
This assumption relaxes the QDI requirements a little further in the quest for performance. The c-element is effectively three gates, the logic, the driver, and the feedback and is non-inverting. This gets to be cumbersome and expensive if there is a need for a large amount of logic. The acknowledgement theorem states that the driver must acknowledge the logic. The half-cycle timing assumption assumes that the driver and feedback will stabilize before the inputs to the logic are allowed to switch.[timing 5] This allows the designer use the output of the logic directly, bypassing the driver and making shorter cycles for higher frequency processing.
Atomic complex gates
A large amount of the automatic synthesis literature uses atomic complex gates. A tree of gates is assumed to transition completely before any of the inputs at the leaves of the tree are allowed to switch again.[timing 6][timing 7] While this assumption allows automatic synthesis tools to bypass the bubble reshuffling problem, the reliability of these gates tends to be difficult to guarantee.
Relative timing
Relative Timing is a framework for making and implementing arbitrary timing assumptions in QDI circuits. It represents a timing assumption as a virtual causality arc to complete a broken cycle in the event graph. This allows designers to reason about timing assumptions as a method to realize circuits with higher throughput and energy efficiency by systematically sacrificing robustness.[timing 8][timing 9]
Representations
Communicating hardware processes (CHP)
Communicating hardware processes (CHP) is a program notation for QDI circuits inspired by Tony Hoare's communicating sequential processes (CSP) and Edsger W. Dijkstra's guarded commands. The syntax is described below in descending precedence.[synthesis 2]
- Skip
skipdoes nothing. It simply acts as a placeholder for pass-through conditions. - Dataless assignment
a+sets the voltage of the nodeato Vdd whilea-sets the voltage ofato GND. - Assignment
a := eevaluates the expressionethen assigns the resulting value to the variablea. - Send
X!eevaluates the expressionethen sends the resulting value across the channelX.X!is a dataless send. - Receive
X?awaits until there is a valid value on the channelXthen assigns that value to the variablea.X?is a dataless receive. - Probe
#Xreturns the value waiting on the channelXwithout executing the receive. - Simultaneous composition
S * Texecutes the process fragmentsSandTat the same time. - Internal parallel composition
S, Texecutes the process fragmentsSandTin any order. - Sequential composition
S; Texecutes the process fragmentsSfollowed byT. - Parallel composition
S || Texecutes the process fragmentsSandTin any order. This is functionally equivalent to internal parallel composition but with lower precedence. - Deterministic selection
[G0 -> S0[]G1 -> S1[]...[]Gn -> Sn]implements choice in whichG0,G1,...,Gnare guards which are dataless boolean expressions or data expressions that are implicitly cast using a validity check andS0,S1,...,Snare process fragments. Deterministic selection waits until one of the guards evaluates to Vdd, then proceeds to execute the guard's associated process fragment. If two guards evaluate to Vdd during the same window of time, an error occurs.[G]is shorthand for[G -> skip]and simply implements a wait. - Non-deterministic selection
[G0 -> S0:G1 -> S1:...:Gn -> Sn]is the same as deterministic selection except that more than one guard is allowed to evaluate to Vdd. Only the process fragment associated with the first guard to evaluate to Vdd is executed. - Repetition
*[G0 -> S0[]G1 -> S1[]...[]Gn -> Sn]or*[G0 -> S0:G1 -> S1:...:Gn -> Sn]is similar to the associated selection statements except that the action is repeated while any guard evaluates to Vdd.*[S]is shorthand for*[Vdd -> S]and implements infinite repetition.
Hand-shaking expansions (HSE)
Hand-shaking expansions are a subset of CHP in which channel protocols are expanded into guards and assignments and only dataless operators are permitted. This is an intermediate representation toward the synthesis of QDI circuits.
Petri nets (PN)
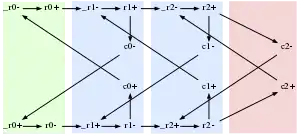
A petri net (PN) is a bipartite graph of places and transitions used as a model for QDI circuits. Transitions in the petri net represent voltage transitions on nodes in the circuit. Places represent the partial states between transitions. A token inside a place acts as a program counter identifying the current state of the system and multiple tokens may exist in a petri net simultaneously. However, for QDI circuits multiple tokens in the same place is an error.
When a transition has tokens on every input place, that transition is enabled. When the transition fires, the tokens are removed from the input places and new tokens are created on all of the output places. This means that a transition that has multiple output places is a parallel split and a transition with multiple input places is a parallel merge. If a place has multiple output transitions, then any one of those transitions could fire. However, doing so would remove the token from the place and prevent any other transition from firing. This effectively implements choice. Therefore, a place with multiple output transitions is a conditional split and a place with multiple input transitions is a conditional merge.
Event-rule systems (ER)
Event-rule systems (ER) use a similar notation to implement a restricted subset of petri net functionality in which there are transitions and arcs, but no places. This means that the baseline ER system lacks choice as implemented by conditional splits and merges in a petri net and disjunction implemented by conditional merges. The baseline ER system also doesn't allow feedback.
While petri nets are used to model the circuit logic, an ER system models the timing and execution trace of the circuit, recording the delays and dependencies of each transition. This is generally used to determine which gates need to be faster and which gates can be slower, optimizing the sizing of devices in the system.[sizing 1]
Repetitive event-rule systems (RER) add feedback by folding the trace back on itself, marking the fold point with a tick mark.[sizing 1] Extended event-rule systems (XER) add disjunction.[sizing 2]
Production rule set (PRS)
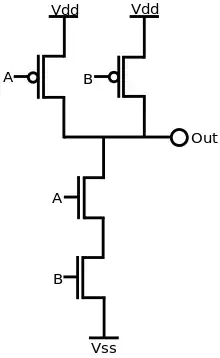
A production rule specifies either the pull-up or pull-down network of a gate in a QDI circuit and follows the syntax G -> S in which G is a guard as described above and S is one or more dataless assignments in parallel as described above. In states not covered by the guards, it is assumed that the assigned nodes remain at their previous states. This can be achieved using a staticizor of either weak or combinational feedback (shown in red). The most basic example is the C-element in which the guards do not cover the states where A and B are not the same value.
Synthesis

Re & Lr -> _Rr- ~_Rr -> Rr+ Rr -> Le- ~Re & ~Lr -> _Rr+ _Rr -> Rr- ~Rr -> Le+

en & Lr -> _Rr- ~_Rr -> Rr+ Lr & Rr -> _Lv- ~_Lv -> Lv+ Lv -> Le- ~Le & ~Re -> _en+ _en -> en- ~en -> _Rr+ _Rr -> Rr- ~Lr & ~Rr -> _Lv+ _Lv -> Lv- ~Lv -> Le+ Le & Re -> _en- ~_en -> en+
There are many techniques for constructing a QDI circuits, but they can generally be classified into two strategies.
Formal synthesis
Formal synthesis was introduced by Alain Martin in 1991.[synthesis 2] The method involves making successive program transformations which are proven to maintain program correctness. The goal of these transformations is to convert the original sequential program into a parallel set of communicating process which each map well to a single pipeline stage. The possible transformations include:
- Projection splits a process which has disparate, non-interacting sets of variables into a separate process per set. [synthesis 3]
- Process decomposition splits a process with minimally interacting variables sets into a separate process per set in which each process communicates to another only as necessary across channels.
- Slack matching involves adding pipeline stages between two communicating processes in order to increase overall throughput. [synthesis 4]
Once the program is decomposed into a set of small communicating processes, it is expanded into hand-shaking expansions (HSE). Channel actions are expanded into their constituent protocols and multi-bit operators are expanded into their circuit implementations. These HSE are then reshuffled to optimize the circuit implementation by reducing the number of dependencies.[synthesis 5] Once the reshuffling is decided upon, state variables are added to disambiguate circuit states for a complete state encoding.[synthesis 6] Next, minimal guards are derived for each signal assignment, producing production rules. There are multiple methods for doing this including guard strengthening, guard weakening, and others.[synthesis 2] The production rules are not necessarily CMOS implementable at this point, so bubble reshuffling moves signal inversions around the circuit in an attempt to make it so. However, bubble reshuffling is not guaranteed to succeed. This is where atomic complex gates are generally used in automated synthesis programs.
Syntax directed translation
The second strategy, syntax directed translation, was first introduced in 1988 by Steven Burns. This seeks a simpler approach at the expense of circuit performance by mapping each CHP syntax to a hand-compiled circuit template.[synthesis 7] Synthesizing a QDI circuit using this method strictly implements the control flow as dictated by the program. This was later adopted by Philips Research Laboratories in their implementation of Tangram. Unlike Steven Burns' approach using circuit templates, Tangram mapped the syntax to a strict set of standard cells, facilitating layout as well as synthesis.[synthesis 8]
Templated synthesis
A hybrid approach introduced by Andrew Lines in 1998 transforms the sequential specification into parallel specifications as in formal synthesis, but then uses predefined pipeline templates to implement those parallel processes similar to syntax-directed translation.[synthesis 9] Andrew outlined three efficient logic families or reshufflings.
Weak condition half buffer (WCHB)
Weak condition half buffer (WCHB) is the simplest and fastest of the logic families with a 10 transition pipeline cycle (or 6 using the half-cycle timing assumption). However, it is also limited to simpler computations because more complex computations tend to necessitate long chains of transistors in the pull-up network of the forward driver. More complex computations can generally be broken up into simpler stages or handled directly with one of the pre-charge families. The WCHB is a half buffer meaning that a pipeline of N stages can contain at most N/2 tokens at once. This is because the reset of the output request Rr must wait until after the reset of the input Lr.
Pre-charge half buffer (PCHB)
Pre-charge half buffer (PCHB) uses domino logic to implement a more complex computational pipeline stage. This removes the long pull-up network problem, but also introduces an isochronic fork on the input data which must be resolved later in the cycle. This causes the pipeline cycle to be 14 transitions long (or 10 using the half-cycle timing assumption).
Pre-charge full buffer (PCFB)
Pre-charge full buffers (PCFB) are very similar to PCHB, but adjust the reset phase of the reshuffling to implement full buffering. This means that a pipeline of N PCFB stages can contain at most N tokens at once. This is because the reset of the output request Rr is allowed to happen before the reset of the input Lr.
Verification
Along with the normal verification techniques of testing, coverage, etc, QDI circuits may be verified formally by inverting the formal synthesis procedure to derive a CHP specification from the circuit. This CHP specification can then be compared against the original to prove correctness. [verification 1][verification 2]
References
Synthesis
- Tse, Jonathan; Hill, Benjamin; Manohar, Rajit (May 2013). "A Bit of Analysis on Self-Timed Single-Bit On-Chip Links" (PDF). 2013 IEEE 19th International Symposium on Asynchronous Circuits and Systems. Proceedings of the 19th IEEE International Symposium on Asynchronous Circuits and Systems (ASYNC). pp. 124–133. CiteSeerX 10.1.1.649.294. doi:10.1109/ASYNC.2013.26. ISBN 978-1-4673-5956-6. S2CID 11196963.
- Martin, Alain (1991). Synthesis of Asynchronous VLSI Circuits (PDF) (Report). California Institute of Technology.
- Manohar, Rajit; Lee, Tak-Kwan; Martin, Alain (1999). "Projection: A synthesis technique for concurrent systems". Proceedings. Fifth International Symposium on Advanced Research in Asynchronous Circuits and Systems (PDF). pp. 125–134. CiteSeerX 10.1.1.49.2264. doi:10.1109/ASYNC.1999.761528. ISBN 978-0-7695-0031-7. S2CID 11051137.
{{cite book}}:|journal=ignored (help) - Manohar, Rajit; Martin, Alain J. (1998-06-15). "Slack elasticity in concurrent computing". Mathematics of Program Construction (PDF). Lecture Notes in Computer Science. Vol. 1422. Springer, Berlin, Heidelberg. pp. 272–285. CiteSeerX 10.1.1.396.2277. doi:10.1007/bfb0054295. ISBN 9783540645917.
- Manohar, R. (2001). "An analysis of reshuffled handshaking expansions" (PDF). Proceedings Seventh International Symposium on Asynchronous Circuits and Systems. ASYNC 2001. pp. 96–105. CiteSeerX 10.1.1.11.55. doi:10.1109/async.2001.914073. ISBN 978-0-7695-1034-7. S2CID 5156531. Archived from the original (PDF) on 2017-10-14.
- Cortadella, J.; Kishinevsky, M.; Kondratyev, A.; Lavagno, L.; Yakovlev, A. (March 1996). "Complete state encoding based on the theory of regions". Proceedings Second International Symposium on Advanced Research in Asynchronous Circuits and Systems (PDF). pp. 36–47. doi:10.1109/async.1996.494436. hdl:2117/129509. ISBN 978-0-8186-7298-9. S2CID 14297152.
- Burns, Steven; Martin, Alain (1988). "Syntax-Directed Translation of Concurrent Programs into Self-Timed Circuits" (PDF). California Institute of Technology.
{{cite journal}}: Cite journal requires|journal=(help) - Berkel, Kees van; Kessels, Joep; Roncken, Marly; Saeijs, Ronald; Schalij, Frits (1991). "The VLSI-programming language Tangram and its translation into handshake circuits" (PDF). Proceedings of the European Conference on Design Automation. IEEE Design Automation. pp. 384–389. doi:10.1109/EDAC.1991.206431. S2CID 34437785.
- Lines, Andrew (1998). "Pipelined Asynchronous Circuits" (PDF) (M.S.). California Institute of Technology. doi:10.7907/z92v2d4z.
{{cite journal}}: Cite journal requires|journal=(help)
Timing
- Martin, Alain J. (1990). "The Limitations to Delay-Insensitivity in Asynchronous Circuits" (PDF). Sixth MIT Conference on Advanced Research in VLSI. MIT Press.
- Manohar, Rajit; Martin, Alain (1995). "Quasi-Delay-Insensitive Circuits are Turing-Complete" (PDF). California Institute of Technology. doi:10.7907/Z9H70CV1.
{{cite journal}}: Cite journal requires|journal=(help) - Manohar, R.; Moses, Y. (May 2015). "Analyzing Isochronic Forks with Potential Causality". 2015 21st IEEE International Symposium on Asynchronous Circuits and Systems (PDF). pp. 69–76. doi:10.1109/async.2015.19. ISBN 978-1-4799-8716-0. S2CID 10262182.
- Keller, S.; Katelman, M.; Martin, A. J. (May 2009). "A Necessary and Sufficient Timing Assumption for Speed-Independent Circuits". 2009 15th IEEE Symposium on Asynchronous Circuits and Systems (PDF). pp. 65–76. doi:10.1109/async.2009.27. ISBN 978-0-7695-3616-3. S2CID 6612621.
- LaFrieda, C.; Manohar, R. (May 2009). "Reducing Power Consumption with Relaxed Quasi Delay-Insensitive Circuits". 2009 15th IEEE Symposium on Asynchronous Circuits and Systems (PDF). pp. 217–226. CiteSeerX 10.1.1.153.3557. doi:10.1109/async.2009.9. ISBN 978-0-7695-3616-3. S2CID 6282974.
- Meng, T. H. Y.; Brodersen, R. W.; Messerschmitt, D. G. (November 1989). "Automatic synthesis of asynchronous circuits from high-level specifications". IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. 8 (11): 1185–1205. doi:10.1109/43.41504. ISSN 0278-0070.
- Pastor, E.; Cortadella, J.; Kondratyev, A.; Roig, O. (November 1998). "Structural methods for the synthesis of speed-independent circuits" (PDF). IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. 17 (11): 1108–1129. doi:10.1109/43.736185. hdl:2117/125785. ISSN 0278-0070.
- Stevens, K. S.; Ginosar, R.; Rotem, S. (February 2003). "Relative timing" (PDF). IEEE Transactions on Very Large Scale Integration (VLSI) Systems. 11 (1): 129–140. doi:10.1109/tvlsi.2002.801606. ISSN 1063-8210.
- Manoranjan, J. V.; Stevens, K. S. (May 2016). "Qualifying Relative Timing Constraints for Asynchronous Circuits". 2016 22nd IEEE International Symposium on Asynchronous Circuits and Systems (ASYNC) (PDF). pp. 91–98. doi:10.1109/async.2016.23. ISBN 978-1-4673-9007-1. S2CID 6239093.
Verification
- Longfield, S. J.; Manohar, R. (May 2013). "Inverting Martin Synthesis for Verification". 2013 IEEE 19th International Symposium on Asynchronous Circuits and Systems (PDF). pp. 150–157. CiteSeerX 10.1.1.645.9939. doi:10.1109/async.2013.10. ISBN 978-1-4673-5956-6. S2CID 762078.
- Longfield, Stephen; Nkounkou, Brittany; Manohar, Rajit; Tate, Ross (2015). "Preventing glitches and short circuits in high-level self-timed chip specifications". Proceedings of the 36th ACM SIGPLAN Conference on Programming Language Design and Implementation (PDF). PLDI '15. New York, NY, USA: ACM. pp. 270–279. doi:10.1145/2737924.2737967. ISBN 9781450334686. S2CID 6363535.
Sizing
- Burns, Steven (1991). Performance Analysis and Optimization of Asynchronous Circuits (Ph.D.). California Institute of Technology.
- Lee, Tak-Kwan (1995). A General Approach to Performance Analysis and Optimization of Asynchronous Circuits (Ph.D.). Defense Technical Information Center.
Layout
- Karmazin, R.; Longfield, S.; Otero, C. T. O.; Manohar, R. (May 2015). "Timing Driven Placement for Quasi Delay-Insensitive Circuits". 2015 21st IEEE International Symposium on Asynchronous Circuits and Systems (PDF). pp. 45–52. doi:10.1109/async.2015.16. ISBN 978-1-4799-8716-0. S2CID 10745504.
Chips
- Martin, Alain; Burns, Steven; Lee, Tak-Kwan (1989). "The design of an asynchronous microprocessor". ACM SIGARCH Computer Architecture News. 17 (4): 99–110. doi:10.1145/71317.1186643.
- Nanya, T.; Ueno, Y.; Kagotani, H.; Kuwako, M.; Takamura, A. (Summer 1994). "TITAC: design of a quasi-delay-insensitive microprocessor" (PDF). IEEE Design and Test of Computers. 11 (2): 50–63. doi:10.1109/54.282445. ISSN 0740-7475. S2CID 9351043.
- Takamura, A.; Kuwako, M.; Imai, M.; Fujii, T.; Ozawa, M.; Fukasaku, I.; Ueno, Y.; Nanya, T. (October 1997). "TITAC-2: An asynchronous 32-bit microprocessor based on scalable-delay-insensitive model". Proceedings International Conference on Computer Design VLSI in Computers and Processors (PDF). pp. 288–294. CiteSeerX 10.1.1.53.7359. doi:10.1109/iccd.1997.628881. ISBN 978-0-8186-8206-3. S2CID 14119246. Archived from the original (PDF) on 2017-10-14.
External links
Tools
- "Petrify: a tool for synthesis of Petri Nets and asynchronous circuits". UPC/DAC VLSI CAD Group. Retrieved 6 October 2017.
- Fang, David. "The Hierarchical Asynchronous Circuit Kompiler Toolkit". Retrieved 6 October 2017.
- "Balsa Asynchronous Synthesis System". GitHub. Retrieved 6 October 2017.
- Manohar, Rajit. "The ACT language and core tools". GitHub. Retrieved 14 February 2020.
- Bingham, Ned (14 February 2020). "HSE Simulator". GitHub. Retrieved 14 February 2020.