Quine–Putnam indispensability argument

The second premise of the indispensability argument states mathematical objects are indispensable to our best scientific theories. In this context, indispensability is not the same as ineliminability because any entity can be eliminated from a theoretical system given appropriate adjustments to the other parts of the system.[22] Therefore, dispensability requires an entity is eliminable without sacrificing the attractiveness of the theory. The attractiveness of the theory can be evaluated in terms of theoretical virtues such as explanatory power, empirical adequacy and simplicity.[23] Furthermore, if an entity is dispensable to a theory, an equivalent theory can be formulated without it.[24] This is the case, for example, if each sentence in one theory is a paraphrase of a sentence in another or if the two theories predict the same empirical observations.[25]

According to the Stanford Encyclopedia of Philosophy, one of the most influential argument against the indispensability argument comes from Hartry Field.[26] It rejects the claim that mathematical objects are indispensable to science;[27] Field has supported this argument by reformulating or "nominalizing" scientific theories so they do not refer to mathematical objects.[28] As part of this project, Field has offered a reformulation of Newtonian physics in terms of the relationships between space-time points. Instead of referring to numerical distances, Field's reformulation uses relationships such as "between" and "congruent" to recover the theory without implying the existence of numbers.[29] John Burgess and Mark Balaguer have taken steps to extend this nominalizing project to areas of modern physics, including quantum mechanics.[30] Philosophers such as David Malament and Otávio Bueno dispute whether such reformulations are successful or even possible, particularly in the case of quantum mechanics.[31]

Field's alternative to platonism is mathematical fictionalism, according to which mathematical theories are false because they make claims about abstract mathematical objects even though abstract objects do not exist.[32] As part of his argument against the indispensability argument, Field has tried to explain how it is possible for false mathematical statements to be used by science without making scientific predictions false.[33] His argument is based on the idea that mathematics is conservative. A mathematical theory is conservative if, when combined with a scientific theory, it does not imply anything about the physical world that the scientific theory alone would not have already.[34] This explains how it is possible for mathematics to be used by scientific theories without making the predictions of science false. In addition, Field has attempted to specify how exactly mathematics is useful in application.[26] Field thinks mathematics is useful for science because mathematical language provides a useful shorthand for talking about complex physical systems.[30]

Another approach to denying that mathematical entities are indispensable to science is to reformulate mathematical theories themselves so they do not imply the existence of mathematical objects. Charles Chihara, Geoffrey Hellman, and Putnam have offered modal reformulations of mathematics that replace all references to mathematical objects with claims about possibilities.[30]

The naturalism underlying the indispensability argument is a form of methodological naturalism, as opposed to metaphysical naturalism, that asserts the primacy of the scientific method for determining the truth.[35] In other words, according to Quine's naturalism, our best scientific theories are the best guide to what exists.[17] This form of naturalism rejects the idea that philosophy precedes and ultimately justifies belief in science, instead holding that science and philosophy are continuous with one another as part of a single, unified investigation into the world.[36] As such, this form of naturalism precludes the idea of a prior philosophy that can overturn the ontological commitments of science.[37] This is in contrast to alternative forms of naturalism, such as a form supported by David Armstrong that holds a principle called the Eleatic principle. According to this principle there are only causal entities and no non-causal entities.[38] Quine's naturalism claims such a principle cannot be used to overturn our best scientific theories' ontological commitment to mathematical entities because philosophical principles cannot overrule science.[39]

Quine held his naturalism as a fundamental assumption but later philosophers have provided arguments to support it. The most common arguments in support of Quinean naturalism are track-record arguments. These are arguments that appeal to science's successful track record compared to philosophy and other disciplines.[40] David Lewis (1991) famously made such an argument in a passage from his 1991 book Parts of Classes, deriding the track record of philosophy compared to mathematics and arguing that the idea of philosophy overriding science is absurd.[41] Critics of the track record argument have argued that it goes too far, discrediting philosophical arguments and methods entirely, and contest the idea that philosophy can be uniformly judged to have had a bad track record.[42]

Quine's naturalism has also been criticized by Penelope Maddy for contradicting mathematical practice.[43] According to the indispensability argument, mathematics is subordinated to the natural sciences in the sense that its legitimacy depends on them.[44] But Maddy (1992) argues mathematicians do not seem to believe their practice is restricted in any way by the activity of the natural sciences. For example, mathematicians' arguments over the axioms of Zermelo–Fraenkel set theory do not appeal to their applications to the natural sciences. Similarly, Charles Parsons has argued that mathematical truths seem immediately obvious in a way that suggests they do not depend on the results of our best theories.[45]

Confirmational holism is the view that scientific theories and hypotheses cannot be confirmed in isolation and must be confirmed together as part of a larger cluster of theories.[46] An example of this idea provided by Michael Resnik is of the hypothesis that an observer will see oil and water separate out if they are added together because they do not mix. This hypothesis cannot be confirmed in isolation because it relies on assumptions such as the absence of any chemical that will interfere with their separation and that the eyes of the observer are functioning well enough to observe the separation.[47] Because mathematical theories are likewise assumed by scientific theories, confirmational holism implies the empirical confirmations of scientific theories also support these mathematical theories.[48]

According to a counterargument by Maddy (1992), the theses of naturalism and confirmational holism that make up the first premise of the indispensability argument are in tension with one another. Maddy said naturalism tells us that we should respect the methods used by scientists as the best method for uncovering the truth, but scientists do not seem to act as though we should believe in all of the entities that are indispensable to science.[49] To illustrate this point, Maddy uses the example of atomic theory; she said that despite the atom being indispensable to scientists' best theories by 1860, their reality was not universally accepted until 1913 when they were put to a direct experimental test.[50] Maddy also appeals to the fact that scientists use mathematical idealizations, such as assuming bodies of water to be infinitely deep without regard for the trueness of such applications of mathematics. According to Maddy, this indicates that scientists do not view the indispensable use of mathematics for science as justification for the belief in mathematics or mathematical entities. Overall, Maddy said we should side with naturalism and reject confirmational holism, meaning we do not need to believe in all of the entities that are indispensable to science.[26]

Another counterargument due to Elliott Sober (1993) claims that mathematical theories are not tested in the same way as scientific theories. Whilst scientific theories compete with alternatives to find which theory has the most empirical support, there are no alternatives for mathematical theory to compete with because all scientific theories share the same mathematical core. As a result, according to Sober, mathematical theories do not share the empirical support of our best scientific theories so we should reject confirmational holism.[51]

Since these counterarguments have been raised, a number of philosophers—including Resnik, Alan Baker, Patrick Dieveney, David Liggins, Jacob Busch, and Andrea Sereni—have argued that confirmational holism can be eliminated from the argument.[52] For example, Resnik (1995, p. 171) has offered a pragmatic indispensability argument that "claims that the justification for doing science ... also justifies our accepting as true such mathematics as science uses".[53]

Another key part of the argument is the concept of ontological commitment. To say that we should have an ontological commitment to an entity means we should believe that entity exists. Quine believed that we should have ontological commitment to all the entities to which our best scientific theories are themselves committed.[54] According to Quine's "criterion of ontological commitment", the commitments of a theory can be found by translating or "regimenting" the theory from ordinary language into first-order logic. This criterion says that the ontological commitments of the theory are all of the objects over which the regimented theory quantifies; the existential quantifier for Quine was the natural equivalent of the ordinary language term "there is", which he believed obviously carries ontological commitment.[55] Quine thought it is important to translate our best scientific theories into first-order logic because ordinary language is ambiguous, whereas logic can make the commitments of a theory more precise. Translating theories to first-order logic also has advantages over translating them to higher-order logics such as second-order logic. Whilst second-order logic has the same expressive power as first-order logic, it lacks some of the technical strengths of first-order logic such as completeness and compactness. Second-order logic also allows quantification over properties like "redness", but whether we have ontological commitment to properties is controversial.[16] According to Quine, such quantification is simply ungrammatical.[56]

Jody Azzouni has objected to Quine's criterion of ontological commitment, saying that the existential quantifier in first-order logic need not be interpreted as always carrying ontological commitment.[57] According to Azzouni, the ordinary language equivalent of existential quantification "there is" is often used in sentences without implying ontological commitment. In particular, Azzouni (2004, pp. 68–69) points to the use of "there is" when referring to fictional objects in sentences such as "there are fictional detectives who are admired by some real detectives".[58] According to Azzouni, for us to have ontological commitment to an entity, we must have the right level of epistemic access to it. This means, for example, that it must overcome some epistemic burdens for us to be able to postulate it. But according to Azzouni (2004, p. 127), mathematical entities are "mere posits" that can be postulated by anyone at any time by "simply writing down a set of axioms", so we do not need to treat them as real.[59]

More modern presentations of the argument do not necessarily accept Quine's criterion of ontological commitment and may allow for ontological commitments to be directly determined from ordinary language.[60][lower-alpha 4]

In his counterargument, Joseph Melia (1998, pp. 70–71) argues that the role of mathematics in science is not genuinely explanatory and is solely used to "make more things sayable about concrete objects".[62] He appeals to a practice he calls weaseling, which occurs when a person makes a statement and then later withdraws something implied by that statement. An example of weaseling is the statement: "Everyone who came to the seminar had a handout. But the person who came in late didn't get one."[63] Whilst this statement can be interpreted as being self-contradictory, it is more charitable to interpret it as coherently making the claim: "Except for the person who came in late, everyone who came to the seminar had a handout."[63] Melia said a similar situation occurs in scientists' use of statements that imply the existence of mathematical objects. According to Melia (2000, p. 489), whilst scientists use statements that imply the existence of mathematics in their theories, "almost all scientists ... deny that there are such things as mathematical objects".[63] As in the seminar-handout example, Melia said it is most charitable to interpret scientists not as contradicting themselves, but rather as weaseling away their commitment to mathematical objects. According to Melia, because this weaseling is not a genuinely explanatory use of mathematical language, it is acceptable to not believe in the mathematical objects that scientists weasel away.[62]

Inspired by Maddy's and Sober's arguments against confirmational holism,[64] as well as Melia's argument that we can suspend belief in mathematics if it does not play a genuinely explanatory role in science,[65] Colyvan and Baker have defended an explanatory version of the argument.[66][lower-alpha 5] This version of the argument attempts to remove the reliance on confirmational holism by replacing it with an inference to the best explanation. It states we are justified in believing in mathematical objects because they appear in our best scientific explanations, not because they inherit the empirical support of our best theories.[69] It is presented by the Internet Encyclopedia of Philosophy in the following form:[66]

• There are genuinely mathematical explanations of empirical phenomena.
• We ought to be committed to the theoretical posits in such explanations.
• Therefore, we ought to be committed to the entities postulated by the mathematics in question.

Number line visualizing why prime-numbered life cycles are advantageous compared to non-prime life cycles. If predators have life cycles of 3 or 4 years, they quickly synchronize with a non-prime life cycle such as a life cycle of 12 years. But they will not synchronize with a 13-year periodical cicada's life cycle until 39 and 52 years have passed, respectively.

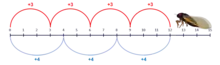
An example of mathematics' explanatory indispensability presented by Baker (2005) is the periodic cicada, a type of insect that has life cycles of 13 or 17 years. It is hypothesized that this is an evolutionary advantage because 13 and 17 are prime numbers. Because prime numbers have no non-trivial factors, this means it is less likely predators can synchronize with the cicadas' life cycles. Baker said that this is an explanation in which mathematics, specifically number theory, plays a key role in explaining an empirical phenomenon.[70] Other important examples are explanations of the hexagonal structure of bee honeycombs, the existence of antipodes on the Earth's surface that have identical temperature and pressure, the connection between Minkowski space and Lorentz contraction, and the impossibility of crossing all seven bridges of Königsberg only once in a walk across the city.[71] The main response to this form of the argument, which philosophers such as Melia, Chris Daly, Simon Langford, and Juha Saatsi adopted, is to deny there are genuinely mathematical explanations of empirical phenomena, instead framing the role of mathematics as representational or indexical.[72]

Aspects of the indispensability argument can be traced back to Gottlob Frege

The argument is historically associated with Willard Quine and Hilary Putnam but it can be traced to earlier thinkers such as Gottlob Frege and Kurt Gödel. In his arguments against mathematical formalism—a view that argues that mathematics is akin to a game like chess with rules about how mathematical symbols such as "2" can be manipulated—Frege (2017, §91) said in 1893 that "it is applicability alone which elevates arithmetic from a game to the rank of a science".[73] Gödel (1947, §3), in a paper on the axioms of set theory, said that if a new axiom were to have enough verifiable consequences, it "would have to be accepted at least in the same sense as any well‐established physical theory".[73] Frege's and Gödel's arguments differ from the later Quinean indispensability argument because they lack features such as naturalism and subordination of practice, leading some philosophers, including Pieranna Garavaso (2005), to say that they are not genuine examples of the indispensability argument.[74]

Whilst developing his philosophical view of confirmational holism, Quine was influenced by Pierre Duhem.[75] At the beginning of the twentieth century, Duhem defended the law of inertia from critics who said that it is devoid of empirical content and unfalsifiable.[47] These critics based this claim on the fact that the law does not make any observable predictions without positing some observational frame of reference and that falsifying instances can always be avoided by changing the choice of reference frame. Duhem responded by saying that the law produces predictions when paired with auxiliary hypotheses fixing the frame of reference and is therefore no different from any other physical theory.[76] Duhem said that although individual hypotheses may make no observable predictions alone, they can be confirmed as parts of systems of hypotheses. Quine extended this idea to mathematical hypotheses, claiming that although mathematical hypotheses hold no empirical content on their own, they can share in the empirical confirmations of the systems of hypotheses in which they are contained.[77] This thesis later came to be known as the Duhem–Quine thesis.[78]

Quine (1981b, p. 67) described his naturalism as the "abandonment of the goal of a first philosophy. It sees natural science as an inquiry into reality, fallible and corrigible but not answerable to any supra-scientific tribunal, and not in need of any justification beyond observation and the hypothetico-deductive method."[79] The term "first philosophy" is used in reference to Descartes' Meditations on First Philosophy, in which Descartes used his method of doubt in an attempt to secure the foundations of science. Quine said that Descartes' attempts to provide the foundations for science had failed and that the project of finding a foundational justification for science should be rejected because he believed philosophy could never provide a method of justification more convincing than the scientific method.[80] Quine was also influenced by the logical positivists, such as his teacher Rudolf Carnap; his naturalism was formulated in response to many of their ideas.[81] For the logical positivists, all justified beliefs were reducible to sense data, including our knowledge of ordinary objects such as trees.[82] Quine criticized sense data as self-defeating, saying that we must believe in ordinary objects to organize our experiences of the world. He also said that because science is our best theory of how sense-experience gives us beliefs about ordinary objects, we should believe in it as well.[83] Whilst the logical positivists said that individual claims must be supported by sense data, Quine's confirmational holism means scientific theory is inherently tied up with mathematical theory and so evidence for scientific theories can justify belief in mathematical objects despite them not being directly perceived.[82]

Whilst he eventually became a platonist due to his formulation of the indispensability argument,[84] Quine was sympathetic to nominalism from the early stages of his career.[85] In a 1946 lecture, he said: "I will put my cards on the table now and avow my prejudices: I should like to be able to accept nominalism" (Quine 2008, p. 6).[86] Nelson Goodman and Quine (1947) subsequently released a joint 1947 paper titled "Steps toward a Constructive Nominalism" as part of an ongoing project of Quine's to "set up a nominalistic language in which all of natural science can be expressed" (Quine 1939, p. 708).[87] In a letter to Joseph Henry Woodger the following year, however, Quine said that he was becoming more convinced "the assumption of abstract entities and the assumptions of the external world are assumptions of the same sort".[88] He later released the 1948 paper "On What There Is", in which he said that "[t]he analogy between the myth of mathematics and the myth of physics is ... strikingly close" (Quine 1948, p. 37), marking a shift towards his eventual acceptance of a "reluctant platonism".[89]

Throughout the 1950s, Quine regularly mentioned platonism, nominalism, and constructivism as plausible views, and he had not yet reached a definitive conclusion about which is correct.[90] It is unclear exactly when Quine accepted platonism; in 1953, he distanced himself from the claims of nominalism in his 1947 paper with Goodman, but by 1956, Goodman (1956) was still describing Quine's "defection" from nominalism as "still somewhat tentative".[91] According to Lieven Decock, Quine had accepted the need for abstract mathematical entities by the publication of his 1960 book Word and Object, in which he wrote "a thoroughgoing nominalist doctrine is too much to live up to" (Quine 1960, p. 269).[92] However, whilst he released suggestions of the indispensability argument in a number of papers, he never gave it a detailed formulation.[93]

Putnam gave the argument its first explicit presentation in his 1971 book Philosophy of Logic in which he attributed it to Quine.[94] He stated the argument as "quantification over mathematical entities is indispensable for science, both formal and physical; therefore we should accept such quantification; but this commits us to accepting the existence of the mathematical entities in question" (Putnam 1971, p. 347).[95] He also wrote Quine had "for years stressed both the indispensability of quantification over mathematical entities and the intellectual dishonesty of denying the existence of what one daily presupposes" (Putnam 1971, p. 347).[95] Putnam's endorsement of Quine's version of the argument is disputed. The Internet Encyclopedia of Philosophy states: "In his early work, Hilary Putnam accepted Quine's version of the indispensability argument."[96] Liggins also states that the argument has been attributed to Putnam by many philosophers of mathematics. Liggins and Bueno, however, said Putnam never endorsed the argument and only presented it as an argument from Quine.[97] Putnam has said he differed with Quine in his attitude to the argument from at least 1975.[98] Features of the argument that Putnam came to disagree with include its reliance on a single, regimented, best theory.[96]

In 1975, Putnam formulated his own indispensability argument based on the no miracles argument in the philosophy of science, which argues the success of science can only be explained by scientific realism without being rendered miraculous. He wrote that year (Putnam 1979, p. 73): "I believe that the positive argument for realism [in science] has an analogue in the case of mathematical realism. Here too, I believe, realism is the only philosophy that doesn't make the success of the science a miracle."[96] The Internet Encyclopedia of Philosophy terms this version of the argument "Putnam's success argument" and presents it in the following form:[96]

• Mathematics succeeds as the language of science.
• There must be a reason for the success of mathematics as the language of science.
• No positions other than realism in mathematics provide a reason.
• Therefore, realism in mathematics must be correct.[lower-alpha 6]

According to the Internet Encyclopedia of Philosophy, the first and second premises of the argument have been seen as uncontroversial, so discussion of this argument has been focused on the third premise. Other positions that have attempted to provide a reason for the success of mathematics include Field's reformulations of science, which explain the usefulness of mathematics as a conservative shorthand.[96] Putnam has criticized Field's reformulations for only applying to classical physics and for being unlikely to be able to be extended to future fundamental physics.[101]

Chihara (1973), in Ontology and the Vicious Circle Principle, was one of the earliest philosophers to attempt to reformulate mathematics in response to Quine's arguments.[102] Field (1980) followed with Science Without Numbers and dominated discussion about the indispensability argument throughout the 1980s and 1990s.[103] With the introduction of arguments against the first premise of the argument, initially by Maddy in the 1990s and continued by Melia and others in the 2000s, Field's approach has come to be known as "Hard Road Nominalism" due to the difficulty of creating technical reconstructions of science that it requires. Approaches attacking the first premise, in contrast, have come to be known as "Easy Road Nominalism".[104]

Colyvan (1998, 2001) is often seen as presenting the standard or "canonical" formulation of the argument within more recent philosophical work.[105] Colyvan's version of the argument has been influential in debates in contemporary philosophy of mathematics.[106] It differs in key ways from the arguments presented by Quine and Putnam. Quine's version of the argument relies on translating scientific theories from ordinary language into first-order logic to determine its ontological commitments whereas the modern version allows ontological commitments to be directly determined from ordinary language. Putnam's arguments were for the objectivity of mathematics but not necessarily for mathematical objects.[107] Putnam has explicitly distanced himself from this version of the argument, saying, "from my point of view, Colyvan's description of my argument(s) is far from right", and has contrasted his indispensability argument with "the fictitious 'Quine–Putnam indispensability argument'".[108] Colyvan has said "the attribution to Quine and Putnam [is] an acknowledgement of intellectual debts rather than an indication that the argument, as presented, would be endorsed in every detail by either Quine or Putnam".[109]